Dynamics II: lecture 3
Gerrit Lohmann date: April 26, 2021
Organization of
Lecture: April 26, 2021 (Monday), 14:00 Prof. Dr. Gerrit Lohmann
Tutorial: April 26, 2021 (Monday), ca. 15:30 Justus Contzen, Lars Ackermann
Time required for Sheet 2: 8 h
Third lecture (link)
Content in the script: Content: Atmosphere and Ocean Dynamics, Scaling of the
dynamical equations, Geostrophy
After the lecture: Read the script about Atmosphere and Ocean Dynamics, Scaling of the dynamical equations, Geostrophy
It might take 80 min.
Rayleigh number Ra: Buoyancy & Viscosity
\[ \mbox{Motion develops if } \quad R_a = \frac{g \alpha H^3 \Delta T}{\nu \kappa} \quad \mbox{exceeds } \quad R_c = \pi^4 \frac{(1+a^2)^3}{a^2} \]
\[ \mbox{The minimum value of $R_c = 657.51$ occurs when $a^2 = 1/2$. } \]
\[ \mbox{When } R_a < R_c,\mbox{ heat transfer is due to conduction} \]
\[ \mbox{When } R_a > R_c, \mbox{ heat transfer is due to convection.} \]
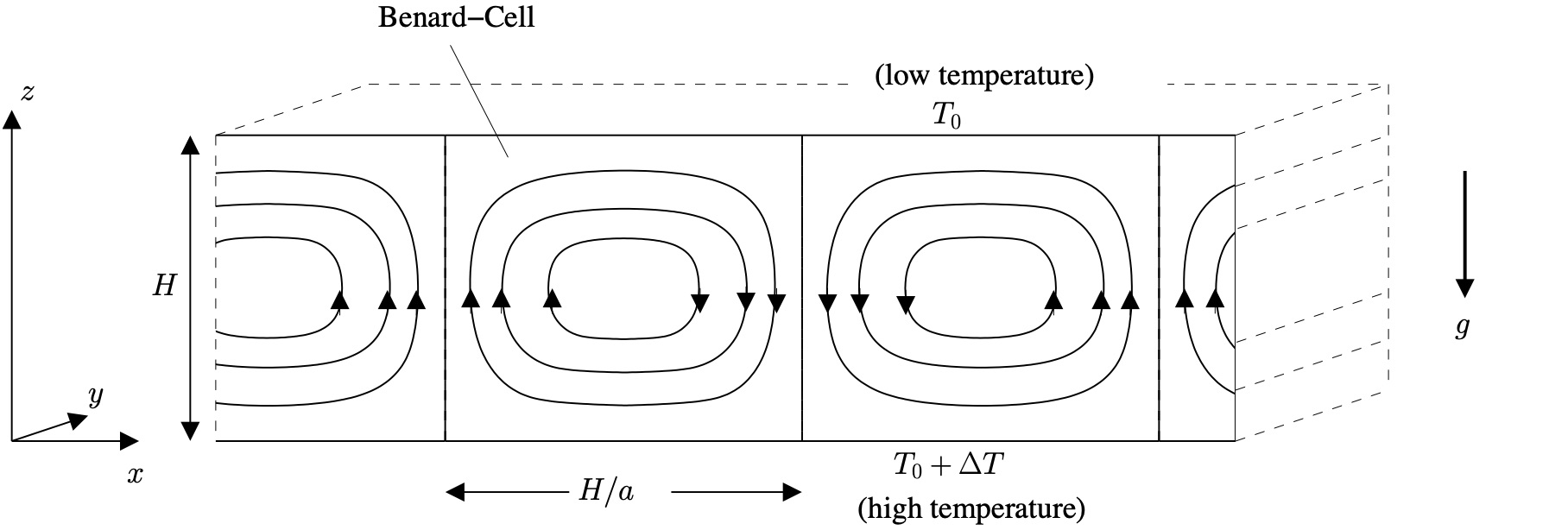
Lorenz system
Bifurcation at \[ r = R_a/R_c = 1 \]
Geometry constant \[ b = 4(1+a^2)^{-1} \]
Famous low-order model:
\[ \dot X = -\sigma X + \sigma Y \]
\[ \dot Y = r X - Y - X Z \]
\[ \dot Z = -b Z + X Y \]
\[ \mbox{dimensionless time } \quad t_d = \pi^2 H^{-2} (1+a^2) \kappa t, \] \[ \mbox{ Prandtl number } \quad \sigma = \nu \kappa^{-1}, \]
Lorenz system r=24
r=24
s=10
b=8/3
dt=0.01
x=0.1
y=0.1
z=0.1
vx<-c(0)
vy<-c(0)
vz<-c(0)
for(i in 1:10000){
x1=x+s*(y-x)*dt
y1=y+(r*x-y-x*z)*dt
z1=z+(x*y-b*z)*dt
vx[i]=x1
vy[i]=y1
vz[i]=z1
x=x1
y=y1
z=z1}
plot(vx,vy,type="l",xlab="x",ylab="y") plot(vy,vz,type="l",xlab="y",ylab="z")
Scaling: Rotating frame of reference
The Coriolis effect is one of the dominating forces for the large-scale dynamics.
\[ \underbrace{\frac{\partial \mathbf{v}}{\partial t}}_{ U/T \sim 10^{-8} } + \underbrace{\mathbf{v} \cdot \nabla \mathbf{v}}_{ U^2/L \sim 10^{-8} }= {\underbrace{- \frac{1}{\rho} \nabla p}_{ \bf \delta P/(\rho L) \sim 10^{-5} } + \underbrace{2 \mathbf{\Omega \times v}}_{ \bf f_0 U \sim 10^{-5} } + \underbrace{fric}_{ \nu U/H^2 \sim 10^{-13}}} \quad \]
where fric denotes the contributions of friction due to eddy stress divergence (\( \sim \nu \nabla^2 \mathbf{v} \)). The values have been taken for the ocean. (-> exercise)
Scaling: Rotating frame of reference
The Coriolis effect is one of the dominating forces for the large-scale dynamics.
\[ \underbrace{\frac{\partial \mathbf{v}}{\partial t}}_{ U/T \sim 10^{-8} } + \underbrace{\mathbf{v} \cdot \nabla \mathbf{v}}_{ U^2/L \sim 10^{-8} }= {\underbrace{- \frac{1}{\rho} \nabla p}_{ \bf \delta P/(\rho L) \sim 10^{-5} } + \underbrace{2 \mathbf{\Omega \times v}}_{ \bf f_0 U \sim 10^{-5} } + \underbrace{fric}_{ \nu U/H^2 \sim 10^{-13}}} \quad \]
where fric is due to eddy stress divergence (\( \sim \nu \nabla^2 \mathbf{v} \)).
Because of the continuity equation \[ U/L \sim W/H \] and horizontal scales are orders of magnitude larger than the vertical ones, \[ W << U . \]
The timescales are related to \[ T \sim L/U \sim H/W \]
Exception for small scales (e.g., ocean convection or cumuls clouds): \[ H \sim L \quad \rightarrow \quad W \sim U \]
Rossby number Ro
\[ \underbrace{\frac{\partial \mathbf{v}}{\partial t}}_{ U/T \sim 10^{-8} } + \underbrace{\mathbf{v} \cdot \nabla \mathbf{v}}_{ U^2/L \sim 10^{-8} } = {\underbrace{- \frac{1}{\rho} \nabla p}_{ \bf \delta P/(\rho L) \sim 10^{-5}} + \underbrace{2 \mathbf{\Omega \times v}}_{ \bf f_0 U \sim 10^{-5} } + \underbrace{fric}_{ \nu U/H^2 \sim 10^{-13}}} \]
\[ Ro = \frac{ \mbox{Inertial (the left hand side)} }{ \mbox{Coriolis term } } \]
\[ Ro = \frac{(U^2/L)}{(f U)} = \frac{U}{f L} \quad \]
characterizes the importance of Coriolis acceleration
Ro is small when the flow is in a so-called geostrophic balance.
The local coordinate system
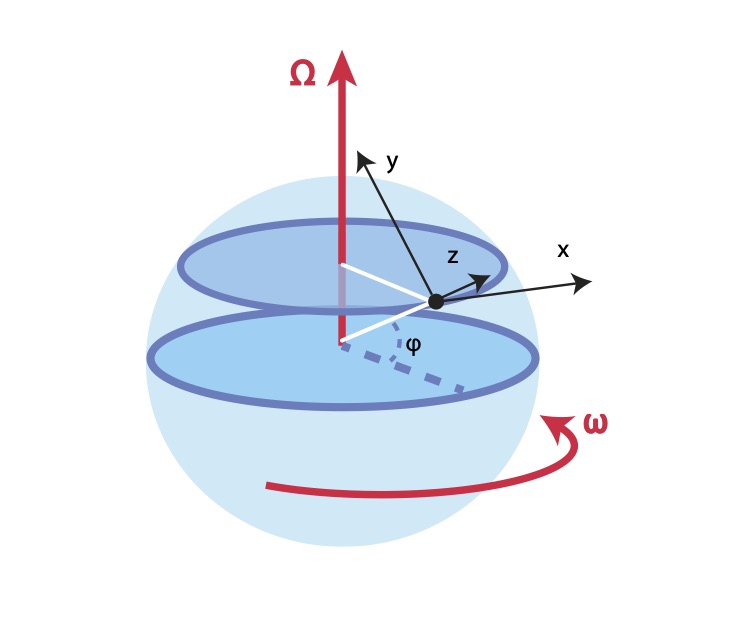
x: east, y: north, z: vertically upwards. \[ (x,y,z)= (a \lambda \cos \varphi, a \varphi, z) \] \( (\lambda,\varphi,z) \) longitude, latitude, height. \( \mbox{Earth radius } a, \Omega \mbox{ rotation } 2 \pi/(24 h) \)
The local coordinate system
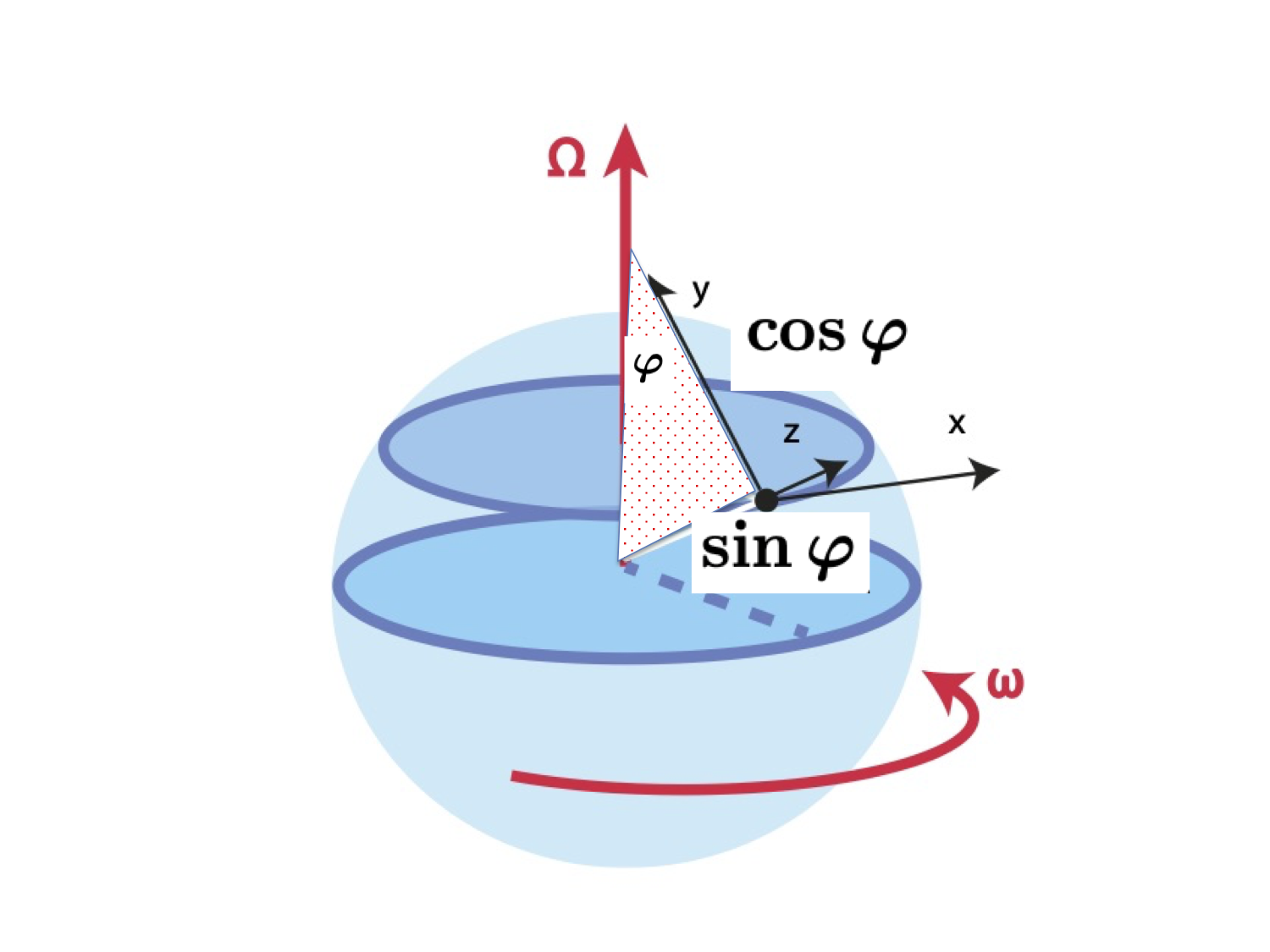
x: east, y: north, z: vertically upwards. \[ (x,y,z)= (a \lambda \cos \varphi, a \varphi, z) \] \( (\lambda,\varphi,z) \) longitude, latitude, height.
\( \mbox{Earth radius } a, \Omega \mbox{ rotation } 2 \pi/(24 h) \)
\[ \mbox{Rotation vector} \quad \boldsymbol{ \Omega} = \Omega \begin{pmatrix} 0 \\ \cos \varphi \\ \sin \varphi \end{pmatrix} \ \]
\[ \mbox{velocity vector} \quad \boldsymbol{ v} = \begin{pmatrix} u \\ v \\ w \end{pmatrix}\ , \]
Coriolis acceleration
\[ \boldsymbol{ a}_C =-2\boldsymbol{\Omega \times v}= 2\,\Omega\, \begin{pmatrix} v \sin \varphi- w \cos \varphi \\ -u \sin \varphi \\ u \cos\varphi\end{pmatrix}\ \]
\[ \mbox{Coriolis parameter: } \, f = 2 \Omega \sin \varphi \, \]
\[ \mbox{2nd Coriolis parameter: } \, f^{(2)}= 2 \Omega \cos \varphi \, \]
Centrifugal term & Gravitational potential
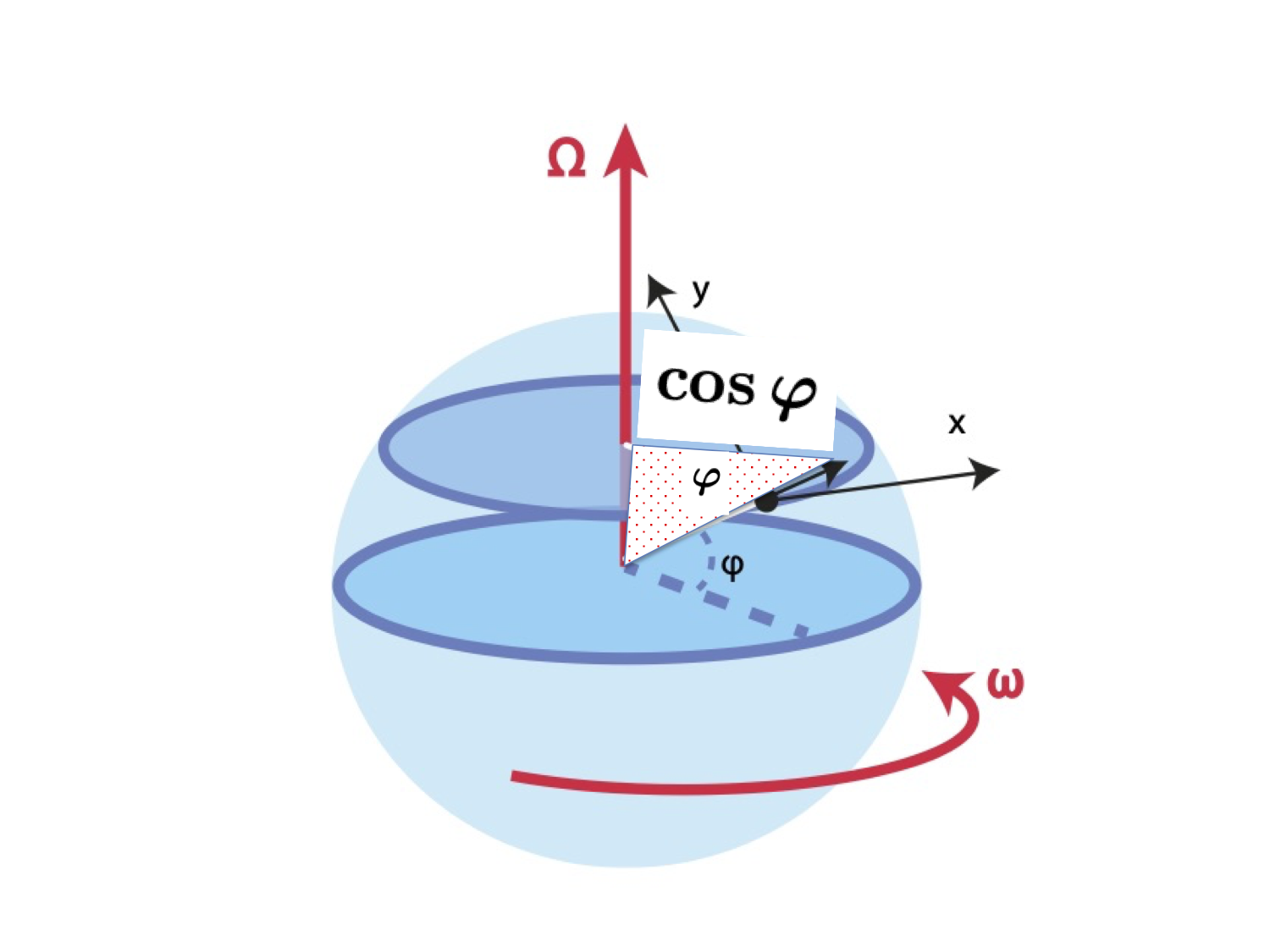
x: east, y: north, z: vertically upwards. \[ (x,y,z)= (a \lambda \cos \varphi, a \varphi, z) \] \( (\lambda,\varphi,z) \) longitude, latitude, height.
\( \mbox{Earth radius } a, \Omega \mbox{ rotation } 2 \pi/(24 h) \)
\[ \boldsymbol{F_{cf}= - \Omega \times( \Omega \times r) } = -\omega^2 \boldsymbol{R }, \]
\[ \boldsymbol{ R} = (a+z) \cos \varphi \] component of \( \boldsymbol{r} \) perpenticular to the axis of rotation
Absorbed into the gravitation “gravity”
Gravitational potential
\[ \phi = g z - \frac{\omega^2 R^2 }{2} = g z - \frac{\omega^2 (a+z)^2 \cos^2 \varphi }{2} \]
Gravity is used for the vertical coordinate
minor modification to gravitation
Coriolis acceleration
\[ \boldsymbol{ a}_C =-2\boldsymbol{\Omega \times v}= 2\,\Omega\, \begin{pmatrix} v \sin \varphi- w \cos \varphi \\ -u \sin \varphi \\ u \cos\varphi\end{pmatrix}\ \approx 2\,\Omega\, \begin{pmatrix} v \sin \varphi \\ -u \sin \varphi \\ u \cos\varphi\end{pmatrix}\ \]
For v = 0 and positive \( \varphi \): movement to the east results in acceleration to south.
For u = 0, a movement due north results in an acceleration due east.
Acceleration always is turned \( 90^\circ \) to the right on the Northern Hemisphere

Momentum equations
\[ \frac{\partial u}{\partial t}+ \mathbf{v} \cdot \nabla u - \, \underbrace{ \frac{u v \tan \varphi }{a} - \frac{u w }{a}}_{\mbox{metric terms} } = - \frac{1}{\rho} \frac{\partial p}{\partial x} + f v - \, \underbrace{ f^{(2)} w}_{\mbox{small}} + \nu \nabla^2 u \]
\[ \frac{\partial v}{\partial t}+ \mathbf{v} \cdot \nabla v - \, \underbrace{ \frac{u^2 \tan \varphi }{a} - \frac{v w }{a}}_{\mbox{metric terms} } = - \frac{1}{\rho} \frac{\partial p}{\partial y} - f u + \nu \nabla^2 v \]
Momentum equations
\[ \frac{\partial u}{\partial t}+ \mathbf{v} \cdot \nabla u - \, \underbrace{ \frac{u v \tan \varphi }{a} - \frac{u w }{a}}_{\mbox{metric terms} } = - \frac{1}{\rho} \frac{\partial p}{\partial x} + f v - \, \underbrace{ f^{(2)} w}_{\mbox{small}} + \nu \nabla^2 u \]
\[ \frac{\partial v}{\partial t}+ \mathbf{v} \cdot \nabla v - \, \underbrace{ \frac{u^2 \tan \varphi }{a} - \frac{v w }{a}}_{\mbox{metric terms} } = - \frac{1}{\rho} \frac{\partial p}{\partial y} - f u + \nu \nabla^2 v \]
complemented by the dynamics for the vertical component
\[ \underbrace{\frac{\partial w}{\partial t}}_{ \begin{smallmatrix} W/T \sim 10^{-11} \end{smallmatrix}} + \underbrace{\mathbf{v} \cdot \nabla w}_{ UW/L \sim 10^{-11} } - \underbrace{\frac{u^2 + v^2 }{a}}_{ U^2/a \sim 10^{-9} } = \underbrace{ - \frac{1}{\rho} \frac{\partial p}{\partial z}}_{ \bf P_0/(\rho H) \sim 10} + \underbrace{ g }_{ \bf \sim 10} + \underbrace{f^{(2)} u}_{ \bf \sim 10^{-5}} + \underbrace{\nu \partial_z^2 w}_{ \nu W/H^2 \sim 10^{-16}} \]
Geostrophy
\[ u_g = \, - \frac{1}{f \rho} \frac{\partial p}{\partial y} \]
\[ v_g = \frac{1}{f \rho} \frac{\partial p}{\partial x} \]
Validity depends on the local Rossby number.
invalid at the equator, because \[ f= 2 \Omega \sin \varphi = 0 \]
Geostrophy
\[ u_g = \, - \frac{1}{f \rho} \frac{\partial p}{\partial y} \]
\[ v_g = \frac{1}{f \rho} \frac{\partial p}{\partial x} \]
Validity depends on the local Rossby number.
invalid at the equator, because \[ f= 2 \Omega \sin \varphi = 0 \]
Large-scale motion:
Perpendicular to the pressure gradient
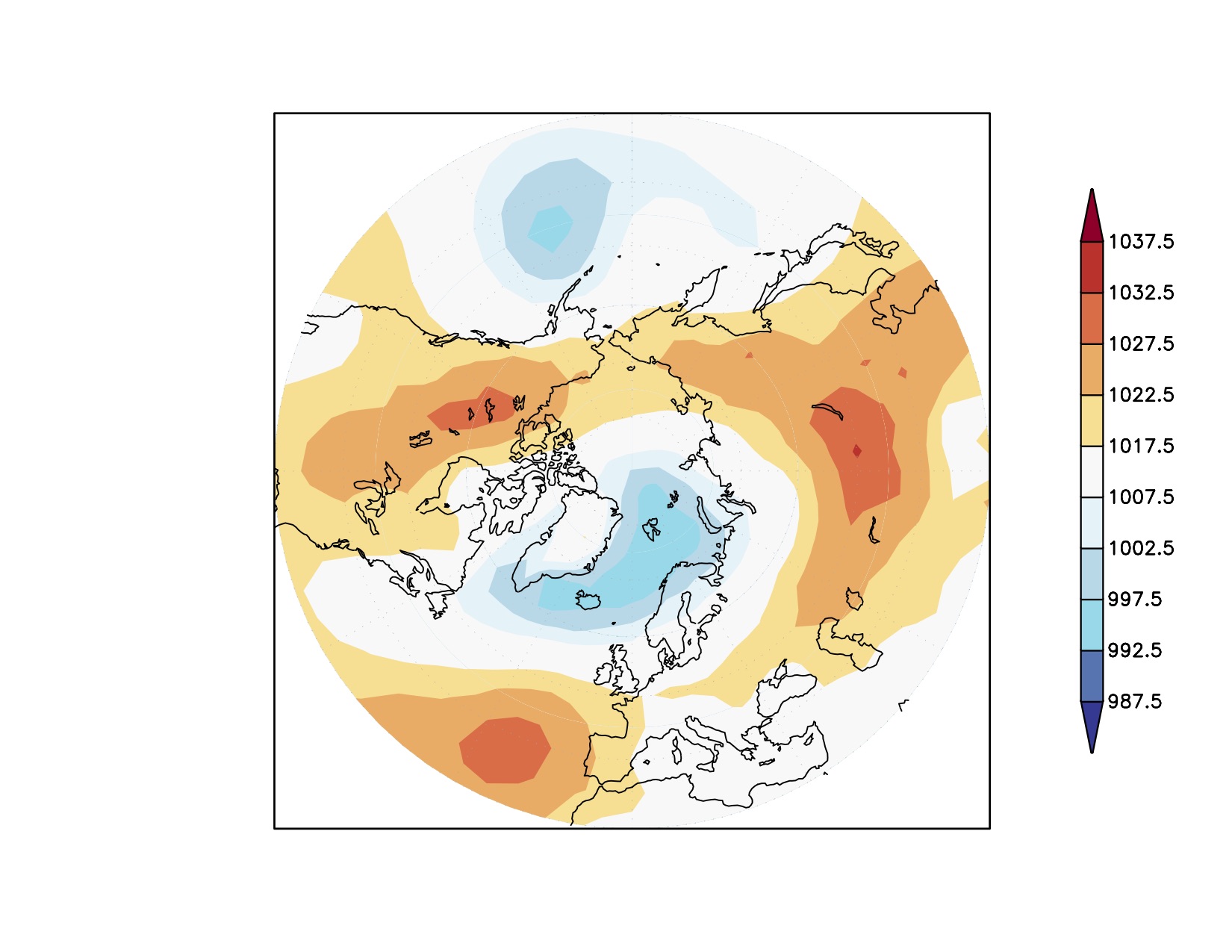
Sea level pressure (hPa) February 2015
Vorticity is the rotation of the fluid
\[ \zeta \equiv \frac{\partial v}{\partial x}-\frac{\partial u}{\partial y} \]
or in 3D:
\[ \equiv \nabla \times \boldsymbol{ u} \]
Vorticity is the rotation of the fluid
\[ \zeta \equiv \frac{\partial v}{\partial x}-\frac{\partial u}{\partial y} \]
or in 3D:
\[ \equiv \nabla \times \boldsymbol{ u} \]
Example: Rigid body rotating
\[ \boldsymbol{ u} = \begin{pmatrix} u \\ v \\ w \end{pmatrix}\ = \boldsymbol{ \Omega} \times \boldsymbol{ r} = \begin{pmatrix} \omega_1 \\ \omega_2 \\ \omega_3 \end{pmatrix}\ \times \ \begin{pmatrix} x \\ y \\ z \end{pmatrix}\ = \begin{pmatrix} \omega_2 z- \omega_3 y\\ \omega_3 x- \omega_1 z \\ \omega_1 y - \omega_2 x \end{pmatrix}\ \]
Rotation vector
\[ \nabla \times \boldsymbol{ u} = \begin{pmatrix} \partial_x \\ \partial_y \\ \partial_z \end{pmatrix}\ \times \ \begin{pmatrix} u \\ v \\ w \end{pmatrix}\ = \begin{pmatrix} \partial_x \\ \partial_y \\ \partial_z \end{pmatrix}\ \times \ \begin{pmatrix} \omega_2 z- \omega_3 y \\ \omega_3 x- \omega_1 z \\ \omega_1 y - \omega_2 x \end{pmatrix}\ \]
Example: Vorticity for a rigid body
Rotation vector
\[ \nabla \times \boldsymbol{ u} = \begin{pmatrix} \partial_x \\ \partial_y \\ \partial_z \end{pmatrix}\ \times \ \begin{pmatrix} u \\ v \\ w \end{pmatrix}\ = \begin{pmatrix} \partial_x \\ \partial_y \\ \partial_z \end{pmatrix}\ \times \ \begin{pmatrix} \omega_2 z- \omega_3 y \\ \omega_3 x- \omega_1 z \\ \omega_1 y - \omega_2 x \end{pmatrix}\ \]
Example: Vorticity for a rigid body in x direction
Rotation vector
\[ \nabla \times \boldsymbol{ u} = \begin{pmatrix} \partial_x \\ \partial_y \\ \partial_z \end{pmatrix}\ \times \ \begin{pmatrix} u \\ v \\ w \end{pmatrix}\ = \begin{pmatrix} \partial_x \\ \underline{\partial_y} \\ \underline{\partial_z} \end{pmatrix}\ \times \ \begin{pmatrix} \omega_2 z- \omega_3 y \\ \underline{\omega_3 x- \omega_1 z} \\ \underline{\omega_1 y - \omega_2 x} \end{pmatrix}\ \]
\[ = \begin{pmatrix} \partial_y (\omega_1 y - \omega_2 x) - \partial_z (\omega_3 x- \omega_1 z ) \\ \\ \\ \end{pmatrix}\ \]
Example: Vorticity for a rigid body in y direction
Rotation vector
\[ \nabla \times \boldsymbol{ u} = \begin{pmatrix} \partial_x \\ \partial_y \\ \partial_z \end{pmatrix}\ \times \ \begin{pmatrix} u \\ v \\ w \end{pmatrix}\ = \begin{pmatrix} \underline{\partial_x} \\ \partial_y \\ \underline{\partial_z} \end{pmatrix}\ \times \ \begin{pmatrix} \underline{\omega_2 z- \omega_3 y } \\ \omega_3 x- \omega_1 z \\ \underline{\omega_1 y - \omega_2 x} \end{pmatrix}\ \]
\[ = \begin{pmatrix} \partial_y (\omega_1 y - \omega_2 x) - \partial_z (\omega_3 x- \omega_1 z ) \\ \partial_z (\omega_2 z- \omega_3 y) - \partial_x (\omega_1 y - \omega_2 x) \\ \\ \end{pmatrix}\ \]
Example: Vorticity for a rigid body in z direction
Rotation vector
\[ \nabla \times \boldsymbol{ u} = \begin{pmatrix} \partial_x \\ \partial_y \\ \partial_z \end{pmatrix}\ \times \ \begin{pmatrix} u \\ v \\ w \end{pmatrix}\ = \begin{pmatrix} \underline{\partial_x} \\ \underline{\partial_y} \\ \partial_z \end{pmatrix}\ \times \ \begin{pmatrix} \underline{\omega_2 z- \omega_3 y} \\ \underline{\omega_3 x- \omega_1 z} \\ \omega_1 y - \omega_2 x \end{pmatrix}\ \]
\[ = \begin{pmatrix} \partial_y (\omega_1 y - \omega_2 x) - \partial_z (\omega_3 x- \omega_1 z ) \\ \partial_z (\omega_2 z- \omega_3 y) - \partial_x (\omega_1 y - \omega_2 x) \\ \partial_x (\omega_3 x- \omega_1 z) - \partial_y (\omega_2 z- \omega_3 y) \end{pmatrix}\ \]
Example: Vorticity for a rigid body
Rotation vector
\[ \nabla \times \boldsymbol{ u} = \begin{pmatrix} \partial_x \\ \partial_y \\ \partial_z \end{pmatrix}\ \times \ \begin{pmatrix} u \\ v \\ w \end{pmatrix}\ = \begin{pmatrix} \partial_x \\ \partial_y \\ \partial_z \end{pmatrix}\ \times \ \begin{pmatrix} \omega_2 z- \omega_3 y \\ \omega_3 x- \omega_1 z \\ \omega_1 y - \omega_2 x \end{pmatrix}\ \]
\[ = \begin{pmatrix} \partial_y (\omega_1 y - \omega_2 x) - \partial_z (\omega_3 x- \omega_1 z ) \\ \partial_z (\omega_2 z- \omega_3 y) - \partial_x (\omega_1 y - \omega_2 x) \\ \partial_x (\omega_3 x- \omega_1 z) - \partial_y (\omega_2 z- \omega_3 y) \end{pmatrix}\ \]
\[ = \begin{pmatrix} \partial_y (\omega_1 y ) - \partial_z (- \omega_1 z ) \\ \partial_z (\omega_2 z) - \partial_x ( - \omega_2 x) \\ \partial_x (\omega_3 x) - \partial_y (- \omega_3 y) \end{pmatrix}\ \]
Example: Vorticity for a rigid body
Rotation vector
\[ \nabla \times \boldsymbol{ u} = \begin{pmatrix} \partial_x \\ \partial_y \\ \partial_z \end{pmatrix}\ \times \ \begin{pmatrix} u \\ v \\ w \end{pmatrix}\ = \begin{pmatrix} \partial_x \\ \partial_y \\ \partial_z \end{pmatrix}\ \times \ \begin{pmatrix} \omega_2 z- \omega_3 y \\ \omega_3 x- \omega_1 z \\ \omega_1 y - \omega_2 x \end{pmatrix}\ \]
\[ = \begin{pmatrix} \partial_y (\omega_1 y - \omega_2 x) - \partial_z (\omega_3 x- \omega_1 z ) \\ \partial_z (\omega_2 z- \omega_3 y) - \partial_x (\omega_1 y - \omega_2 x) \\ \partial_x (\omega_3 x- \omega_1 z) - \partial_y (\omega_2 z- \omega_3 y) \end{pmatrix}\ \]
\[ = \begin{pmatrix} \partial_y (\omega_1 y ) - \partial_z (- \omega_1 z ) \\ \partial_z (\omega_2 z) - \partial_x ( - \omega_2 x) \\ \partial_x (\omega_3 x) - \partial_y (- \omega_3 y) \end{pmatrix}\ = \begin{pmatrix} \omega_1 + \omega_1 \\ \omega_2 + \omega_2 \\ \omega_3 + \omega_3 \end{pmatrix}\ = 2 \boldsymbol{ \Omega} \]
Example: Vorticity from shear
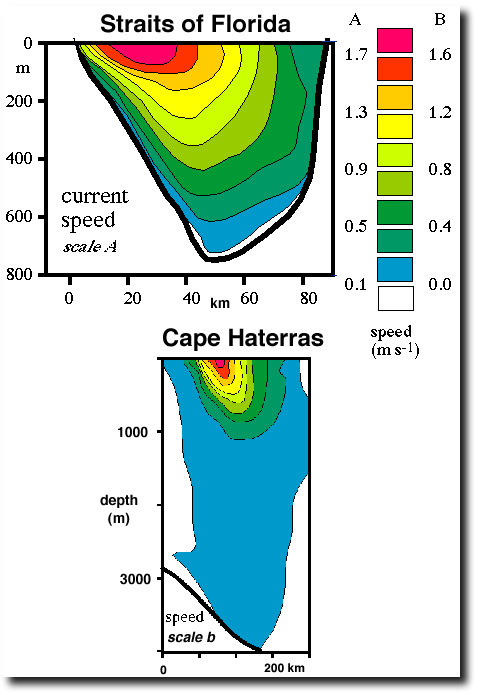
Tomczak & Godfrey: Regional Oceanography
\[ u=0, v=v\left(x\right) \]
\[ \zeta= \partial v\left(x\right)/\partial x \]
Estimate for \( \zeta \) off Cape Hatteras:
the velocity changes by \( 1 \, {m}{s}^{-1} \) in 100 km
\[ \zeta= \frac{\partial v}{\partial x} = \frac{ 1 \, {m}{s}^{-1}}{100 \, {km}} = 10^{-5} \, \frac{1}{s} \]
still much smaller than
\[ f= 2 \Omega \sin \varphi = 2 \, \frac{2 \pi}{day} \sin \varphi \approx \, 10^{-4} \, \frac{1}{s} \]
Planetary and relative vorticity
\[ \mbox{Absolute Vorticity }\equiv\left(\zeta+f\right) \]
\[ \frac{Du}{Dt}-f\;v = -\frac{1}{\rho}\frac{\partial p}{\partial x} \] \[ \frac{Dv}{Dt}+f\;u = -\frac{1}{\rho}\frac{\partial p}{\partial y} \]
Planetary and relative vorticity
\[ \mbox{Absolute Vorticity }\equiv\left(\zeta+f\right) \]
\[ \frac{Du}{Dt}-f\;v = -\frac{1}{\rho}\frac{\partial p}{\partial x} \] \[ \frac{Dv}{Dt}+f\;u = -\frac{1}{\rho}\frac{\partial p}{\partial y} \]
\[ \mbox{subtract } \partial/\partial y \mbox{ of (u-equation) from } \partial /\partial x \mbox{ of (v-equation) } \]
Use \[ \frac{D}{Dt} f = v \, \partial_y f: \]
to obtain
\[ \underline{ \frac{D}{Dt}\left(\zeta+f\right) + \left(\zeta + f\right)\left(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\right)=0 } \quad \]
Examples for Vorticity: Ocean with depth h(x,y)
\[ \mbox{Because of the continuity equation } \quad \partial_x \left( u h \right) + \partial_y \left( v h \right) \quad = \quad 0 \]
\[ \quad \frac{D}{Dt} h + h \left( \partial_x u + \partial_y v \right) = \quad 0 \]
Therefore, \[ \underline{ \frac{D}{Dt}\left(\zeta+f\right) + \left(\zeta + f\right)\left(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\right)=0 } \quad \]
\[ \frac{D}{Dt}\left(\zeta +f\right)-\frac{\left(\zeta+f\right)}{h}\frac{Dh}{Dt}=0 \]
\[ \frac{1}{h} \frac{D}{Dt}\left(\zeta+f\right) - \left(\zeta + f\right) \frac{D_t h}{h^2} =0 \]
\[ \underline{ \frac{D}{Dt}\left( \frac{\zeta+f}{h}\right) = 0 } \quad \]
Potential vorticity is conserved along a fluid trajectory.
Conservation of Vorticity
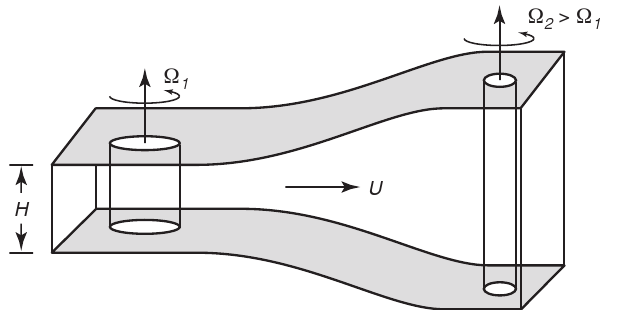
Sketch of the production of relative vorticity by change in the height of a fluid column. As the vertical fluid column moves from left to right, vertical stretching reduces the moment of inertia of the column, causing it to spin faster.
Source: Steward, Oceanography
Conservation of Vorticity

Sketch of the production of relative vorticity by change in the height of a fluid column. As the vertical fluid column moves from left to right, vertical stretching reduces the moment of inertia of the column, causing it to spin faster.
Source: Steward, Oceanography
\[ \frac{D}{Dt}\left( \frac{\zeta+f}{h}\right) = 0 \]
The conservation of potential vorticity couples changes in depth, relative vorticity, and changes in latitude.
Conservation of Vorticity

Sketch of the production of relative vorticity by change in the height of a fluid column. As the vertical fluid column moves from left to right, vertical stretching reduces the moment of inertia of the column, causing it to spin faster.
Source: Steward, Oceanography
\[ \frac{D}{Dt}\left( \frac{\zeta+f}{h}\right) = 0 \]
The conservation of potential vorticity couples changes in depth, relative vorticity, and changes in latitude.
– Changes in the depth h of the flow results in change of the relative vorticity. The concept is analogous with the way figure skaters decrease their spin by extending their arms and legs. The action increases their moment of inertia and decreases their rate of spin
– Changes in latitude require a corresponding change in \( \zeta \). As the water moves equatorward, f decreases, and \( \zeta \) must increase
Conservation of Vorticity
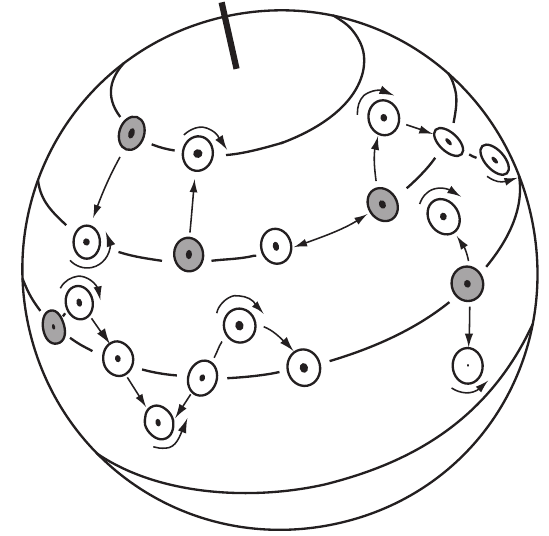
Vorticity tends to be conserved as columns of water change latitude. After von Arx (1962).
\[ \frac{D}{Dt}\left( \zeta+f\right) = 0 \]
Conservation of Vorticity

Vorticity tends to be conserved as columns of water change latitude. After von Arx (1962).
\[ \frac{D}{Dt}\left( \zeta+f\right) = 0 \]
we consider a barrel of water at rest close to the north pole. If the barrel is moved southward, the water in it retains the rotation it had at the pole, and it will appear to rotate counterclockwise at the new latitude where f is smaller.
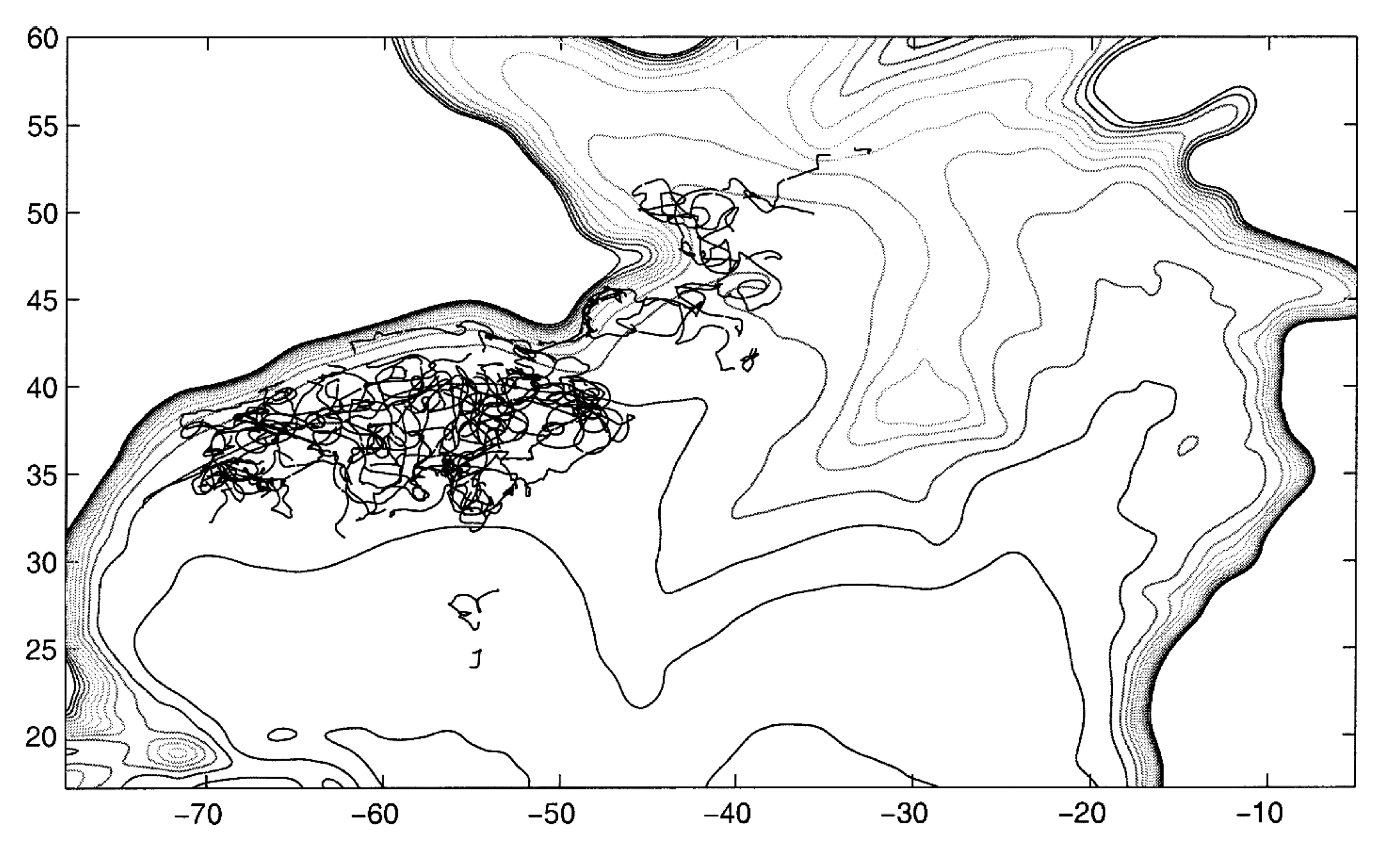
Flow Tends to be Zonal
In the ocean: \[ f >> \zeta \] and thus \[ \frac{D}{Dt}\left( \frac{f}{h}\right) = 0 \]
flow in an ocean of constant depth be zonal.
Contours \( f/h \): combination of latitude circles and bottom topography
Over small horizontal distances, h tends to dominate,
over longer distances, the latitude-variation of f dominates.
Barotropic flow over a ridge is turned equatorward
Topographic Steering at sub-sea ridge
As the depth decreases, \( \zeta+f \) must also decrease, which requires that f decrease, and the flow is turned toward the equator.
If the change in depth is sufficiently large, no change in latitude will be sufficient to conserve potential vorticity, and the flow will be unable to cross the ridge.
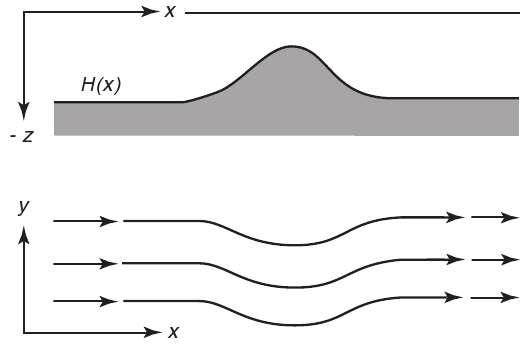
Dietrich et al. (1980)
Taylor-Proudman Theorem
\[ \mbox{Assume constant density } \rho_0 \mbox{ on a plane with constant rotation } f=f_0 \] \[ -f\;v = - \frac{1}{\rho_0} \frac{\partial p}{\partial x} \] \[ f\;u= -\frac{1}{\rho_0} \frac{\partial p}{\partial y} \] \[ g= -\frac{1}{\rho_0}\frac{\partial p}{\partial z} \] \[ \mbox{and the continuity equation is:} \quad 0=\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z} \]
Taking z-derivative of the first \[ -f_0\frac{\partial v}{\partial z}=-\frac{1}{\rho_0}\frac{\partial}{\partial z}\left(\frac{\partial p}{\partial x}\right)=\frac{\partial}{\partial x}\left(-\frac{1}{\rho_0}\frac{\partial p}{\partial z}\right)=\frac{\partial g}{\partial x}=0 \] \[ \mbox{ Therefore for } f_0 \neq 0 \quad \frac{\partial v}{\partial z}=0, \frac{\partial u}{\partial z}=\frac{\partial v}{\partial z}=0 \] Flow is two-dimensional and does not vary in the vertical direction.