Often data matrices have 2 distinct dimensions that correspond to different physical units. For example, suppose we have ${\bf A}_{M\times N}$ representing monthly surface air temperatures along the
35$^\circ$N parallel at fixed spatial intervals over N/12 years. The column M-vector ${\bf a}_j$ comprising all space points at time j is ${\bf A}$'s jth column, $j=1,2\cdots N$ for the N times. Using the SVD representation ${\bf A}={\bf U\Sigma V}^T$ we get the modes of ${\bf A}$; ${\bf U}$'s columns are ${\bf A}$'s EOFs, while ${\bf V}$'s columns are the corresponding `principal components'. (For this reason, in some fields the exact same analysis is called `principal component analysis'.) Given the above arrangement of ${\bf A}$, with time running along the rows and space running along the columns (which is a very common convention), ${\bf U}$'s columns span ${\bf A}$'s column space, which corresponds to the spatial dimension. They are ${\bf A}$'s EOFs. Similarly, ${\bf V}$'s columns span ${\bf A}$'s row space, which corresponds to the timeseries at a given spatial location. Because the modes are arranged in descending order ( $\sigma_i>\sigma_{i+1}$), ${\bf u}_1$, ${\bf U}$'s 1st column, is the spatial pattern most frequently realized, the 2nd is the spatial pattern orthogonal to ${\bf U}$'s 1st column that is most frequently realized, and so on.


 
 

Examples will clarify matters. Consider the signal

\begin{displaymath}f(x,y) = A\; cos\left(\frac{2\pi x}{196}\right)\; cos\left(\... ...{2\pi x}{ 98}\right)\; cos\left(\frac{2\pi y}{ 50}\right) + \xi\end{displaymath}

with

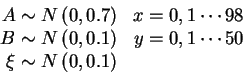
\begin{displaymath}\begin{array}{rr} A \sim N\left(0,0.7\right) & x = 0,1 \cdots... ...y = 0,1 \cdots 50 \\ \xi\sim N\left(0,0.1\right) & \end{array}\end{displaymath}


  
Figure 1: Four spatial patterns used to generate the combined synthetic signal discussed in the text.
\begin{figure}\centerline{\psfig{file=eof1.ps,width=5in}} \end{figure}

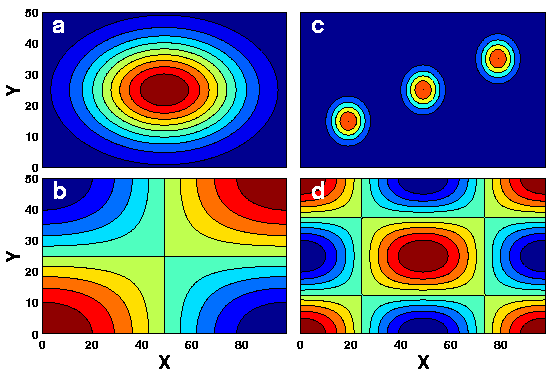
The signal is thus a linear combination of (primarily) the first rhs term (because A's variance is 7 times larger than other additive terms), (some of) the 2nd rhs term, and unstructured noise $\xi(x,y)$. The 2 deterministic patterns are shown in Fig. 1, panels b and d. Note that they are mutually orthogonal (the cosines in both x and y are Fourier frequencies).

Now imagine 50 such f(x,y) fields (xy maps representing random combinations of the 2 patterns plus noise as given above), or a series of $51\times 98$ matrices ${\bf F}_i, \;\;i=1,2\cdots 50$. This is meant to simulate a geophysical situation in which a certain time-dependent field, say sea-level pressure, is generated by some known, deterministic, physics, plus other, low-amplitude, processes, collectively represented here as $\xi(x,y,t)$. Given 50 realizations of this process, we want to identify the dominant spatial patterns of ${\bf F}$, or, put differently, the spatial structures of ${\bf F}$that are most frequently realized.

To identify these structures, we first make the 3-dimensional array ${\bf F}(t)=\left\{ F_{ij}^k \right\}$ (where i is the latitude index, j is the longitude index, and k is the time index) into a 2-dimensional array (matrix), by storing an entire field in one column vector. That is

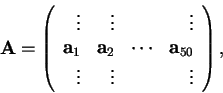
\begin{displaymath}{\bf A}=\left(\begin{array}{rrrr} \vdots & \vdots & & \vdots ... ... {\bf a}_{50} \\ \vdots & \vdots & & \vdots \end{array}\right),\end{displaymath}

where each of ${\bf A}$'s columns, ${\bf a}_k$, comprises the Fijk for all i and j of a given k. The order of the reshaping of each of the ${\bf F}^k$ matrices into a single column vector is not important (MATLAB does it column-wise, but the row-wise reshaping is also perfectly legitimate, as long as you remember how to undo it later. Let's choose to do it the MATLAB (column-wise) way, which, with

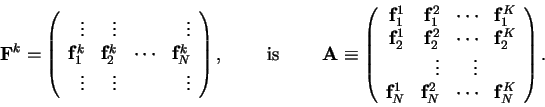
\begin{displaymath}{\bf F}^k=\left(\begin{array}{rrrr} \vdots & \vdots & & \vdo... ...f}_N^1 & {\bf f}_N^2 & \cdots & {\bf f}_N^K \end{array}\right).\end{displaymath}

Now all the information we have about ${\bf F}$is condensed into a single matrix, ${\bf A}$. If we next use ${\bf A}$'s SVD representation, ${\bf A}={\bf U\Sigma V}^T$, and reshape ${\bf U}$'s columns in a manner exactly opposite to the one we employed while forming ${\bf A}$ from ${\bf F}$, we get ${\bf F}$'s EOFs. The kth EOF is in ${\bf u}^k$, ${\bf U}$'s kth column;

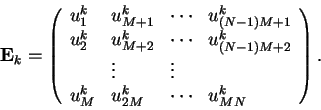
\begin{displaymath}{\bf E}_k=\left(\begin{array}{llll} u_1^k & u_{M+1}^k & \cdot... ...s & \\ u_M^k & u_{2M}^k & \cdots & u_{MN}^k \end{array}\right).\end{displaymath}

Note that the actual numbers (${\bf E}$'s elements) have essentially no interpretable meaning; it is only their relative magnitudes, and signs, that identify the spatial structures of potentially important physical processes.


  
Figure 2: The 3 leading spatial modes (EOFs) of 2 signals. The left panels are for the signal comprising cosines only. The right panels show the EOFs of the signal with both cosine and exponential terms, as described in the text.
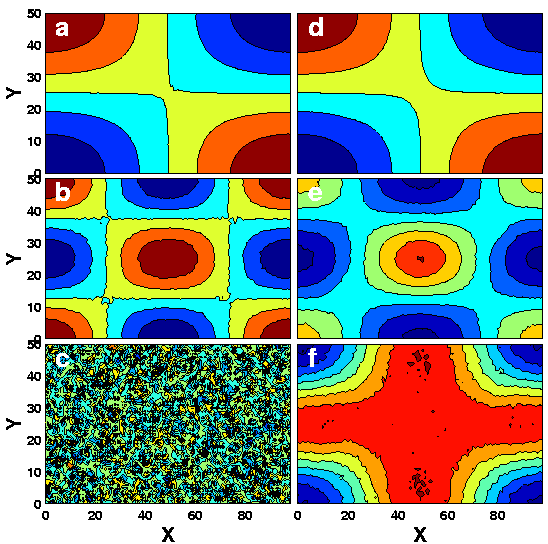\begin{figure}\centerline{\psfig{file=eof2.ps,width=5in}} \end{figure}

To demonstrate the method in action, let's use the 50 fields of the above f(x,y,t), generated from the patterns shown in Fig. 1b and d. Fig. 2a, b and c show the 3 leading EOFs of the cosine signal. Note how both generating patterns are well reproduced by the method (the leading 2 patterns), despite the noise and the random blending of the the signals by the amplitudes A and B. Note also the sign reversal, which is completely immaterial - the singular values (and hence the EOFs and Principal Components) are all known to within a sign, as they are the square root of the eigenvalues of ${\bf AA}^T$ and ${\bf A}^T{\bf A}$. Clearly, the 3rd pattern, a lot like a Jackson Pollock painting, is structureless noise.

A possible critique of the previous example is that we made the method's job particularly (and artificially) easy by using 2 mutually orthogonal generating patterns. This can be fair - if the method is designed to turn arbitrary signals into an orthogonal decomposition of those signals, the real test of the method is with non-orthogonal signals.

To test this, we use the signal

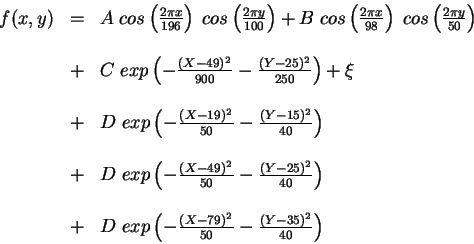
\begin{displaymath}\begin{array}{lcl} f(x,y) & = & A\; cos\left(\frac{2\pi x}{19... ...(-\frac{(X-79)^2}{50} - \frac{(Y-35)^2}{40} \right) \end{array}\end{displaymath}

with $C\sim D\sim N\left(0,0.1\right)$. While this expression certainly looks hideously complicated, it is, in fact, simply a noisy random blend of the four patterns of Fig. 1. Thus the only difference from the previous EOF analysis is that now we add both orthogonal and non-orthogonal components, to address the possible weakness of our previous analysis. Fig. 2d-f show that the method functions well even when the input signal is not artificially orthogonal. The 2 leading modes are nicely reproduced with good fidelity (compared with the generating patterns). The 3rd, while clearly structured (unlike the case with the 2 orthogonal cosines), is a combination of the generating patterns, not an individual pattern. This is the consequence of the non-orthogonality of the exponential generating patterns. Since they are not orthogonal either to each other or to the cosines, they project on them, resulting in the blend shown in Fig. 2f.


  
Figure 3: The singular spectra of the 2 synthetic cases discussed in the text. The empty blue diamonds are for the cosines-only case, while the solid red circles are for the case with all 4 generating patterns.
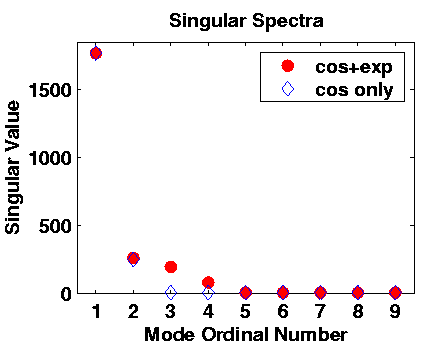\begin{figure}\centerline{\psfig{file=eof3.ps,width=4in}} \end{figure}

It is always extremely important to examine the fraction of the total variance the various modes account for. For the 2 synthetic cases above, this is shown in Fig. 3. (Note that only the leading 9 are shown, of of the 50 total. The rest are very near zero in both cases.) The cosine signals are very similar in both (modes 1 and 2). Higher modes differ. In the cosine only, where the only reminder is noise, it is roughly equally distributed over the entire spectrum. Conversely, in the case of the added exponentials, the remainder has 2 structured modes (the 2 exponential terms, and indeed the singular values 3 and 4 are distinct from zero. The rest, just like in the pure cosine case, are statistically indistinguishable from zero.


  
Figure 4: Leading mode of the winter 700 mb geopotential height anomalies over the Atlantic sector during the indicated period.
\begin{figure}\centerline{\psfig{file=f1.ps,width=5.6in}} \end{figure}

Note that the decrease in amplitude with mode number (the falloff of the singular spectrum) is a property of the analysis, and does not always contain useful information. There is a substantial body of literature about the issue of the appropriate cutoff of the singular spectrum, beyond which, it is assumed, there is little or no useful information. The most commonly used cutoff rule in geophysics is the so-called `Rule N', which basically retains only those modes whose amplitudes stand out above the population of singular spectra extracted from a large number of synthetic matrices of the same dimensions as the one being tested. We will not treat this issue here.


  
Figure 5: The singular spectrum of the observed winter (DJF) 700 mb geopotential height anomalies between 1958 and 2000.
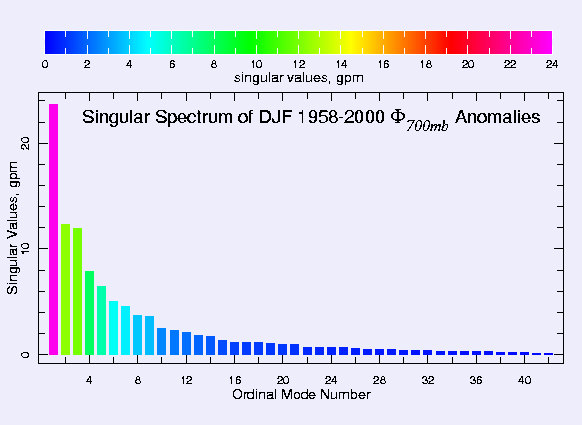\begin{figure}\centerline{\psfig{file=svZ7.ps,width=5.6in}} \end{figure}

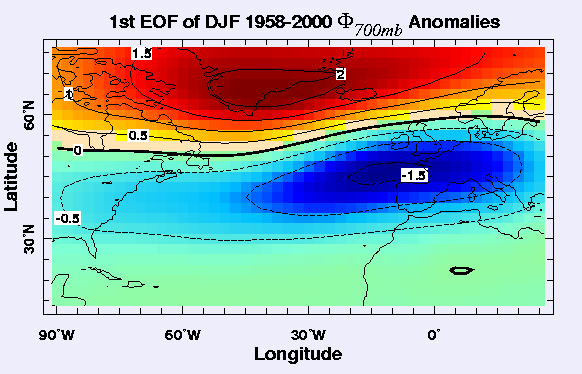
Finally, Fig. 4 shows an example of a real-life use of EOFs. Height anomalies within this domain (which encompasses $\sim$5000 grid points) obviously display a very rich spectrum of variability in time and space. And yet, when piped through the EOF algorithm, a very clear and coherent large scale structure emerges. This information is corroborated by Fig. 5, where the singular spectrum falloff clearly singles out the gravest mode as substantially more important than the 2nd mode, accounting for approximately twice as much variance.