S-mode

The vectors are written as $\vec{x}$ and matrices are denoted by using the capital letters: $X = \left[ \vec{x_1}, \vec{x_2}, .. , \vec{x_T} \right]$ . The vector quantities are used to represent several observations at a given time, i.e. they can be regarded as maps. Let the number of observers mean the number of grid points or stations where observations are made (number of observers = R), and the number of observations be the length of the time series at each location (number of observations = T). We use the notation $\overline{x}$ to mean the temporal mean of x and $\langle x \rangle$ the spatial (ensemble) mean of x.

Let the matrix ${\bf X}_{rt}$ contain T observations from R different locations, where ${\bf X}$ can be expressed in the form ${\bf X} = \left[ \vec{x_1}, \vec{x_2}, .. , \vec{x_T} \right]$ and
$\vec{x_t} = \left[x_1(t), x_2(t), .. ,x_R(t)\right]$ . Each column represents one set of observations, with each element holding the data from the r different locations:

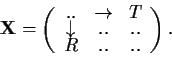$\begin{displaymath}{\bf X} = \left( \begin{array}{ccc} .. & \rightarrow & T \\ \downarrow & .. & .. \\ R & .. & .. \end{array} \right). \end{displaymath}$

(8.2)

Let anomalies in ${\bf X}$ be defined as:

$\begin{displaymath}{\bf X}_{rt}' = {\bf X}_{rt} - \frac{1}{T} \Sigma_{t=1}^{T} {\bf X}_{rt} = {\bf X}_{rt} - \overline{{\bf X}_r}. \end{displaymath}$

(8.3)

The variance-covariance matrix is defined as

$\begin{displaymath}{\bf C}_{rr} = X' {X'}^T = \left( \begin{array}{ccc} .. & \r... ...\\ \downarrow & .. & ..\\ R & .. & .. \end{array} \right). \end{displaymath}$

(8.4)

The S-mode Empirical Orthogonal Functions (EOFs) of ${\bf X}_{rt}$ are defined as:

$\begin{displaymath}{\bf C}_{rr} \vec{e_s} = \lambda \vec{e_s}. \end{displaymath}$

(8.5)

Let ${\bf E}_s = \left[ \vec{e_1}, \vec{e_2}, .. , \vec{e_{R^*}} \right]$ be a matrix with the columns holding the eigenvectors (EOFs) and R^* be the rank of ${\bf X}$ . The data may be expressed in terms of the orthogonal set spanned by the EOFs:

$\begin{displaymath}{\bf F} = {\bf E Y}. \end{displaymath}$

(8.6)

where ${\bf Y}$ is the projection of F onto the EOF space.

We can use singular value decomposition (SVD, see Numerical recipes [], p.61) to compute the EOFs. Using SVD, we can express the matrix ${\bf X}'$ as:

$\begin{displaymath}{\bf X}' = {\bf U W V}^T. \end{displaymath}$

(8.7)

Note that the SVD algorithm is written in such a way that the numbers of columns must be less than number of rows.

In this example, the number of observers is assumed to be greater than the number of observations (which often is the case for gridded climate data). If the number of columns is greater than the number of rows, then the SVD must be applied to the transpose of the matrix ( ${\bf U}$ and ${\bf V}$ will now by swapped).

The columns of ${\bf U}$ and ${\bf V}$ are orthogonal respectively:

$\begin{displaymath}{\bf U}^T {\bf U} = {\bf V}^T {\bf V} = {\bf I}. \end{displaymath}$

(8.8)

The matrix ${\bf W}$ is a diagonal matrix, with R^* non-zero singular values and R - R^* zero values in descending order along the diagonal. The inverse of ${\bf W}$ is a diagonal matrix with the reciprocal of the non-zero singular values along the diagonal. The reciprocal of the small singular values or zeros are taken to be zero.

The variance-covariance matrix can be expressed in terms of the SVD products:

$\begin{displaymath}{\bf C}_{rr} = {\bf X}' {\bf X'}^T = {\bf U W V}^T ( {\bf U W... ...T)^T = {\bf U W V}^T ( {\bf V W U}^T) = {\bf U W}^2 {\bf U}^T. \end{displaymath}$

(8.9)

A right operation of ${\bf U}$ gives:

$\begin{displaymath}{\bf C}_{rr} {\bf U} = {\bf U W}^2. \end{displaymath}$

(8.10)

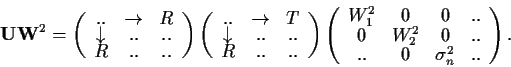$\begin{displaymath}{\bf U W}^2 = \left( \begin{array}{ccc} .. & \rightarrow & R... ...2^2 & 0 & ..\\ .. & 0 & \sigma_n^2& .. \end{array} \right) . \end{displaymath}$

(8.11)

$\begin{displaymath}{\bf C}_{rr} \vec{u} = \sigma^2 \vec{u}. \end{displaymath}$

(8.12)

Hence, ${\bf U}={\bf E}_s$ and $\sigma_i^2 = {\bf W}$ , and the SVD routine applied to ${\bf X}$ gives the S-mode EOFs of ${\bf X}$ .

The S-mode, described above, has been employed where spatial EOF maps have been in focus.