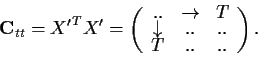T-mode*

The spatial variance-covariance matrix is defined as


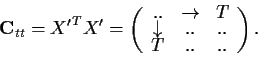\begin{displaymath}{\bf C}_{tt} = {X'}^T X' = \left( \begin{array}{ccc} .. & \r... ...\\ \downarrow & .. & ..\\ T & .. & .. \end{array} \right). \end{displaymath} (8.13)

The T-mode Empirical Orthogonal Functions (EOFs) of ${\bf X}_{rt}$ are defined as:


\begin{displaymath}{\bf C}_{tt} \vec{e_t} = \lambda \vec{e_t}. \end{displaymath} (8.14)

The spatial variance-covariance matrix can be expressed in terms of the SVD products:


\begin{displaymath}{\bf C}_{tt} = {\bf X'}^T {\bf X}' = ( {\bf U W V}^T)^T {\bf U W V}^T = ( {\bf V W U}^T) {\bf U W V}^T = {\bf V W^2 V}^T. \end{displaymath} (8.15)

A right operation of ${\bf V}$ gives:


\begin{displaymath}{\bf C}_{tt} {\bf V} = {\bf V W}^2. \end{displaymath} (8.16)

Hence, ${\bf V}={\bf E}_t$ and $\sigma_i^2 = {\bf W}$, and the SVD routine applied to ${\bf X}$ also gives the T-mode EOFs of ${\bf X}$.

The T-mode has been employed where temporal evolution of coherent spatial structures have been discussed.

The SVD method extract both the S- and T-modes, whereas the eigenvector solutions only give either or. The T-mode forms the basis for both canonical correlation analysis (CCA) and regression.