Example of use: Spatial correlation maps based on EOF products


  
Figure: A comparison between correlation maps between $\Phi _{500hPa}(60^\circ N,5^\circ E)$ and $\Phi _{500hPa}(x,y)$, based on EOFs (a) and conventional calculations (b). The confidence limit for panel b was estimated using the an MC-test on the point of maximum correlation. Note, that the confidence limits are generally higher for the conventional method, whereas only the lowest correlations in panel a are insignificant. [stats_uib_8_4.m]
\begin{figure}\centerline{ \epsfxsize=5in \epsfysize=3in \epsffile{figs/stats_uib_8-4.eps} } \end{figure}

By computing the EOFs and retaining a few of the first leading EOFs ( $n_{eofs} \ll n_t$), one can compress the size of the data from $n_x \times n_y \times n_t$ to $n_x \times n_y \times n_{eofs} + (n_t+1) \times n_{eofs}$ with a minimal loss of information (filters away much of the small-scale noise). If we have a $\Phi _{500hPa}$ record, such as in Fig. 8.4, stored as 100 time slices on a $50 \times 30$ grid and we retain the 10 leading EOFs, then the data size can be reduced from 150,000 numbers to just 16,010 numbers and still account for about 90% of the variance in $\Phi _{500hPa}$.

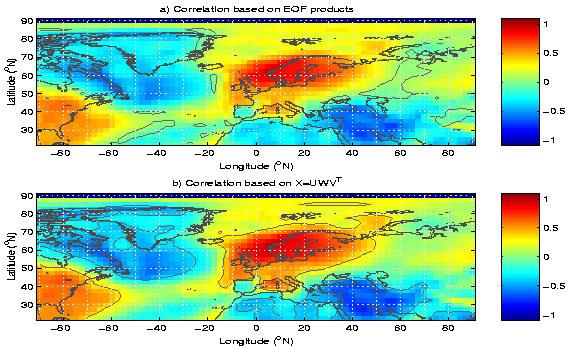
In addition to reducing the data size, the EOFs can save computation time since there are only neofs independent numbers. For instance correlation analysis can be applied to the neofs PCs, weighted by the EOF patterns and their variance, instead of the time series from $n_x \times n_y$ points. The subscripts used below are the location vector $\vec{r}$, the EOF index k and the time index t.


 \begin{displaymath}r({\bf X}_{\vec{r},t},y_t)= \frac{\sum_t \left[ {\bf X}'_{\ve... ...\sqrt{\sum_t ({\bf X'}_{\vec{r},t})^2 \times \sum_t (y'_t)^2}} \end{displaymath} (8.17)


\begin{displaymath}{\bf X}'_{\vec{r},t} = {\bf U}_{\vec{r},k} {\bf W}_k {\bf V}_{k,t}^T \end{displaymath}

${\bf W}_k$ is a diagonal matrix


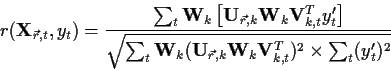
\begin{displaymath}r({\bf X}_{\vec{r},t},y_t)= \frac{\sum_t {\bf W}_k \left[ {\b... ...ec{r},k} {\bf W}_k {\bf V}_{k,t}^T)^2 \times \sum_t (y'_t)^2}} \end{displaymath}


 \begin{displaymath}r({\bf X}_{\vec{r},t},y_t)= \frac{{\bf W}_k {\bf U}_{\vec{r},... ...2 {\bf W}_k^2\sum_t ({\bf V}_{k,t}^2) \times \sum_t (y'_t)^2}} \end{displaymath} (8.18)

The EOFs also allow better confidence limit estimates, as a confidence interval can be computed for each of the neofs PC. The geographically distributed confidence levels may be computed with a similar spatial weighting as the correlations themselves. For MC-test, using EOF products greatly reduces the computation time.

Maps of linear trends can be estimated in a simpler fashion: ${\bf X}_{\mbox{\tiny trend}} = {\bf U}_{\vec{r},k}{\bf W}_k \mbox{\bf trend}_{k,t}^T$. The EOF products are also often used in regressional analysis and CCA.