Dynamics II: lecture 2
Gerrit Lohmann date: April 19, 2021
Summary of last lecture
- Fluid Dynamics, Non-dimensional parameters
- Dynamical similarity
- Elimination of the pressure term and vorticity
After the lecture: Read the script Chapter 1: Basics of Fluid Dynamics
Video Introduction to Atmospheric Dynamics (47 min)
based on Chapter 1 from Holton and Hakim (2013)
Read associated Chapter 1 in
Non-dimensional parameters: Reynolds number
Conservation of mass \[ \nabla_d \cdot \mathbf{u_d} = 0 \] Conservation of momentum
\[ \frac{\partial}{\partial t_d } \mathbf{u_d} + ( \mathbf{u_d} \cdot \nabla_d) \mathbf{u_d} = - \nabla_d p_d + \frac{1}{Re} \nabla_d^2 \mathbf{u_d} \]
The dimensionless parameter \[ Re=UL/ \nu \]
is the Reynolds number and the only parameter left!
For large Reynolds numbers, the flow is turbulent. \( Re \sim (10^4-10^8) \). Flow develops steep gradients locally.
Today: Rayleigh number for Rayleigh-Bénard convection
Preparation: Videos Rayleigh-Benard convection
Experiments:
trailer Cellules de Bénard (1min), Rayleigh–Bénard convection: cooking oil and small aluminium particles (5 min), Was haben Benard-Zellen mit Kochen zu tun? (3 min, German)
Simulations:
Rayleigh Benard Thermal
Convection with LBM (5 min),
Rayleigh Benard Thermal
Convection 3D Simulation (2 min)
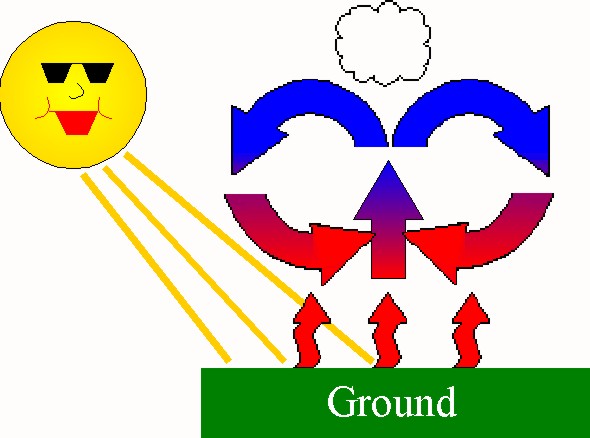
 sketch
sketch
Mathematical concept of bifurcation: Instability
Bifurcation youtube,
Bifurcation Khan academy,
Bifurcation K
Max and Moritz, not lazy,
sawing secretly a gap in the bridge.
When now this act is over, you suddenly hear a scream:
“Hey, out! You billy goat!
Tailor, tailor, bitch, bitch, bitch!”

Stability - Instability: Tailor Böck
And there he is on the bridge,
Cracks! The bridge is falling apart;

Schneider Böck has a fast stream flowing in front of his house. M & M taunt him by making goat noises, until he runs outside. The bridge breaks; the tailor is swept away and nearly drowns (but for two geese, which he grabs a hold of).
Stability - Instability
A typical example could be the consumer-producer problem where the consumption is proportional to the (quantity of) resource.
For example:
\[ \frac{dx}{dt}= \underbrace{r x \cdot \left( 1- x \right)}_{growth} \quad - \quad \underbrace{ \, p \quad x \, }_{consumption} \]
where \[ rx(1-x) \]
is the logistic equation of resource growth:
Rate of reproduction proportional to the population, and available resources
\[ x_{E 1} = 0 \qquad \]
\[ x_{E 2 } = 1 - \frac{p}{r} \]
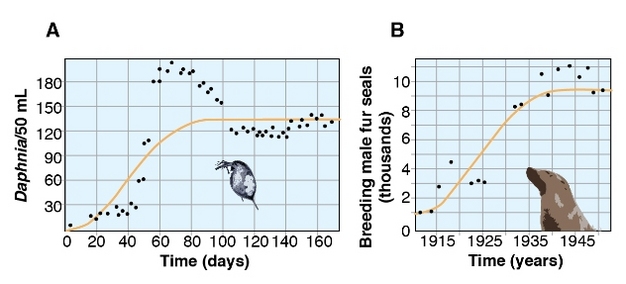
Verhulst: Self-limiting growth
Biological population with size N:
\[ \frac{dN}{dt}=r N \cdot \left( 1- \frac{N}{K} \right) \]
r growth rate and K carrying capacity.
the early, unimpeded growth rate is modeled by the first term \( r N. \)
“Bottleneck” is modeled by the value of K.
As the population grows, \( -r N^2/K \) becomes large as some members interfere with each other by competing for some critical resource (food, living space). The competition diminishes the combined growth rate, until the value of N ceases to grow (maturity of the population).
\[ N(t) = \frac{K N_0 e^{rt}}{K + N_0 \left( e^{rt} - 1\right)} = \frac{K }{K/N_0 e^{-rt} + 1- e^{-rt} } \quad \rightarrow_{t\to \infty } K \]
In climate, the logistic equation is also important for Lorenz's forecast error.
Human population: logistic growth model
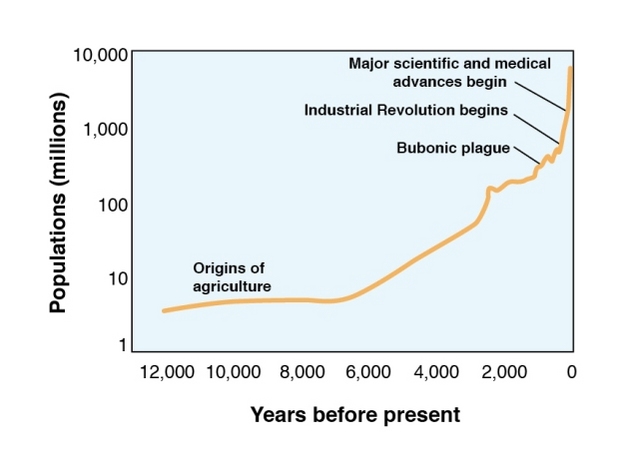
Explosion of human population over the last 10,000 years along with some relevant historical events.
Think about the ways that each of these events might have affected birth and death rates of the human population.
Coronavirus epidemic: logistic growth model
N is the number of cases,
r infection rate,
p cure rate,
K final epidemic size.
dN/dt linearly decreases with the number of cases.
\[ \frac{dN}{dt}=r N \cdot \left( 1- \frac{N}{K} \right) - p N \]
Questions:
When is the growth rate peak?
How many infections ?
When do we need places in hospitals?
Coronavirus epidemic: logistic growth model
Using \[ x = N/K \]
\[ \frac{dx}{dt}= f(x) = \underbrace{r x \cdot \left( 1- x \right)}_{growth} \quad - \quad \underbrace{ p x }_{cure} \]
Without any medicine: \[ r = 3 p \]
\[ x_{E 1} = 0, \mbox{ and } x_{E 2 } = 1 - \frac{p}{r} = 2/3 \]
Stability: f'(x) at \( x_E \)
\[ f'(x) = r - 2 r x -p \]
\[ f'(x_{E 1})= r-p > 0 \quad \mbox{instability} \]
\[ f'(x_{E 2})= -r+p < 0 \quad \mbox{stability} \]
r=2000/150000
r=2000/150000
Bev=85000000
K=1
dt=0.01
N=150000/Bev
vN=c(0); vNp=c(0); vt=c(0)
vN[1]=N; vNp[1]=0; vt[1]=0
for(i in 2:100000){
N1=N+r*N*(1-N/K)*dt
vNp[i]=r*N*(1-N/K)
vN[i]=N1
vt[i]=i*dt
N=N1}
plot(vt,vN,type="l",xlab="time [days]",ylab="N(t)")
plot(vt,vNp*Bev/100,type="l",xlab="time [days]",ylab="dN(t)/dt * 1/100 ")
max(vNp[]*Bev/100)
[1] 2833.333
r=5000/150000
r=5000/150000
Bev=85000000
K=1
dt=0.01
N=10000/Bev
vN=c(0); vNp=c(0); vt=c(0)
vN[1]=N; vNp[1]=0; vt[1]=0
for(i in 2:100000){
N1=N+r*N*(1-N/K)*dt
vNp[i]=r*N*(1-N/K)
vN[i]=N1
vt[i]=i*dt
N=N1}
plot(vt,vN,type="l",xlab="time [days]",ylab="N(t)")
plot(vt,vNp*Bev/100,type="l",xlab="time [days]",ylab="dN(t)/dt * 1/100 ")
max(vNp[]*Bev/100)
[1] 7083.333
Organization of
Lecture: April 19. (Monday), 14:00 Prof. Dr. Gerrit Lohmann
Tutorial: April 19. (Monday), Justus Contzen and Lars Ackermann
Time required for Sheet 2: 8-9 h
April 19, 14:00: Lecture 2 (online G. Lohmann, 45 min)
klick here for the zoom session
Second lecture (link to pdf will become available here)
Content in the script: Rayleigh-Bénard convection, Lorenz system,
nonlinear dynamics, bifurcations, multiple
equilibria
After the lecture: Read the script about [Fluid-dynamical Examples and
Stability Theory (Chapter 2) ](http://paleodyn.uni-bremen.de/study/Dyn2/dyn2script_chapter2.pdf) Reading/learning (the sections with a star are voluntary). It might take 90-120 min.
Linear stability analysis
Consider the continuous dynamical system described by
\[ \dot x=f(x,\lambda)\quad \]
A bifurcation occurs at \[ (x_E,\lambda_0) \]
if the Jacobian matrix
\[ \textrm{d}f/dx (x_E,\lambda_0) \]
has an Eigenvalue with zero real part.
Local analysis !
Linear stability analysis
Consider the continuous dynamical system described by \[ \dot x=f(x,\lambda)\quad \] A bifurcation occurs at \[ (x_E,\lambda_0) \] if the Jacobian matrix \[ \textrm{d}f/dx (x_E,\lambda_0) \] has an Eigenvalue with zero real part.
Example: transcritical bifurcation
a fixed point interchanges its stability with another fixed point as the control parameter is varied. Bifurcation at \( r=0 \).
\[ \frac{dx}{dt}=rx (1-x) \, \]
The two fixed points are 0 and 1. When r is negative, the fixed point at 0 is stable and 1 is unstable. But for \( r>0 \), 0 is unstable and 1 is stable.
Saddle-node bifurcation: two fixed points collide
The normal form: \[ \frac{dx}{dt}=b+x^2 \]
\[ b<0: \mbox{ a stable equilibrium point at } -\sqrt{-b} \mbox{ and an unstable one at } \sqrt{-b} \qquad \qquad \]
\( b=0 \): exactly one equilibrium point, saddle-node fixed point.
\( b>0 \): no equilibrium points. Saddle-node bifurcations may be associated with hysteresis loops.
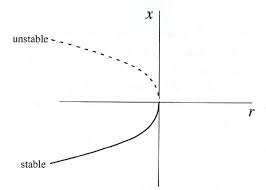
Saddle-node bifurcation: two fixed points collide
1) Calculate the equilibrium points:
\[ f(x) = b + x^2 = 0 \]
\[ x_{E1,E2} = \pm \sqrt{-b} \mbox{ for } b \le 0 \]
2) Linear stability conditions for the equilibrium points
\[ f'(x) = 2x \]
\[ f'(x_{E1}) = 2\sqrt{-b} > 0 \quad \mbox{unstable} \]
\[ f'(x_{E2}) = -2\sqrt{-b} < 0 \quad \mbox{stable} \]
For b=0: equilibrium point \( x_E=0 \) which is indifferent (not stable/unstable).
Saddle-node bifurcation: two fixed points collide
3) Potential or Lyapunov Method
\[ \frac{dx}{dt}=b+x^2 = - \frac{d}{dx} \left( - b x - \frac{x^3}{3} \right) = - \frac{d}{dx} V (x) \]
Global analysis including basins of attraction for \( x_{E2}: (-\infty,3) \)
4) Graphical method: slope at equilibrium points
\[ \frac{dx}{dt}=b+x^2 \]
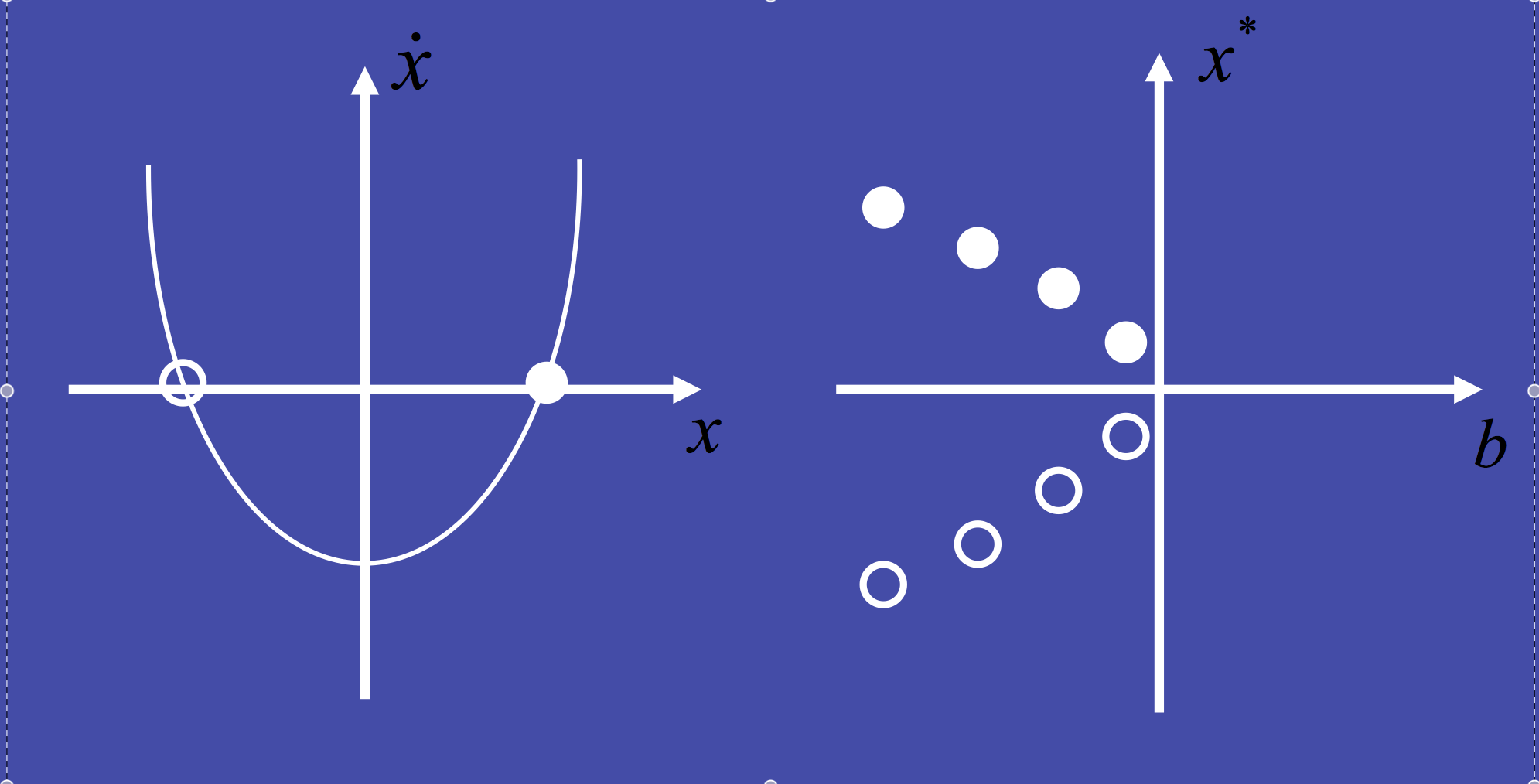
filled points: positive slope => unstable
open points: negative slope => stable
Convection in the Rayleigh-Benard system
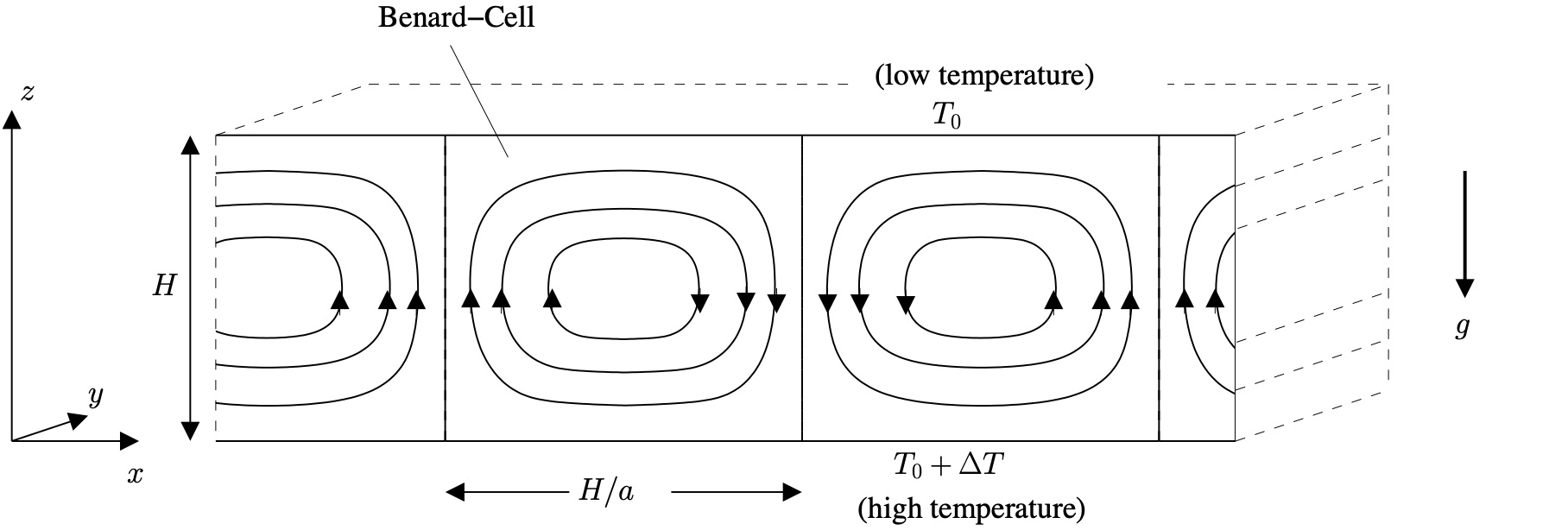
Rayleigh (1916) temperature difference between the upper- and lower-surfaces \[ T(x, y, z=H) = \, T_0 \] \[ T(x, y, z=0) \, = \, T_0 + \Delta T \]
Furthermore \[ \rho = \rho_0 = const. \] except in the buoyancy term, where:
\[ \varrho = \varrho_0 (1 - \alpha(T-T_0)) \mbox{ with } \alpha > 0 \quad . \]
common feature of geophysical flows
No Convection Equilibrium: Diffusion

Diffusion: Temperature varies linearly with depth:
\[ T_{eq} = T_0 + \left(1 - \frac{z}{H}\right) \Delta T \]
No movement of particles:
\[ u = w= 0 \]
When this solution becomes unstable, convection should develop.
Vorticity in the Rayleigh-Benard system
\[ D_t u = - \frac{1}{\rho_0} \partial_x p + \nu \nabla^2 u \label{eqref:einse} \qquad \qquad \qquad \qquad \qquad \qquad (1) \]
\[ D_t w = - \frac{1}{\rho_0} \partial_z p + \nu \nabla^2 w + g (1- \alpha (T-T_0)) \qquad \qquad (2) \]
\[ \partial_x u + \partial_z w = 0 \qquad \qquad \qquad \qquad \qquad \qquad \qquad (3) \]
\[ D_t T = \kappa \nabla^2 T \qquad \qquad \qquad \qquad \qquad \qquad \qquad (4) \]
Introduce vorticity to have (1,2,3) in one equation:
\[ D_t \left( \nabla^2 \Psi\right) = \nu \nabla^4 \Psi - g \alpha \frac{\partial \Theta}{\partial x} \]
Temperature in the Rayleigh-Benard system
\[ T_{eq} = T_0 + \left(1 - \frac{z}{H}\right) \Delta T \]
\[ \mbox{with } \quad T = T_{eq} + \Theta \quad , \quad \mbox{where } \quad \Theta \quad \mbox{is the anomaly} \]
In vorticity equation:
\[ \quad T \frac{\partial }{\partial x} g (1- \alpha (T_{eq} + \Theta -T_0)) = - g \alpha \frac{\partial }{\partial x} \Theta \]
Temperature in the Rayleigh-Benard system
\[ T_{eq} = T_0 + \left(1 - \frac{z}{H}\right) \Delta T \]
\[ \mbox{with } \quad T = T_{eq} + \Theta \quad , \quad \mbox{where } \quad \Theta \quad \mbox{is the anomaly} \]
In vorticity equation:
\[ \frac{\partial }{\partial x} g (1- \alpha (T_{eq} + \Theta -T_0)) = - g \alpha \frac{\partial }{\partial x} \Theta \]
Temperature equation:
\[ D_t T = D_t T_{eq} + D_t \Theta = w \cdot \frac{- \Delta T}{H} + D_t \Theta = - \frac{\Delta T}{H} \frac{\partial \Psi}{\partial x} + D_t \Theta \]
\[ D_t \Theta \quad = \frac{\Delta T}{H} \frac{\partial \Psi}{\partial x} + \kappa \nabla^2 \Theta \quad \]
Non-dimensional Rayleigh-Benard system
\[ \frac{1}{T} \frac{1}{L^2} \frac{L^2}{T} D_t \left( \nabla_d^2 \Psi_d\right) = \nu \frac{1}{L^4} \frac{L^2}{T} \nabla_d^4 \Psi_d - g \alpha \frac{ \Delta T}{L} \frac{\partial \Theta_d}{\partial x_d} \]
\[ \frac{\Delta T}{T} D_t \Theta_d \quad = \frac{\Delta T}{H} \frac{L^2}{ T L} \frac{\partial \Psi_d}{\partial x_d} + \kappa \frac{\Delta T}{L^2} \nabla_d^2 \Theta_d \quad \]
Non-dimensional Rayleigh-Benard system
\[ \frac{1}{T} \frac{1}{L^2} \frac{L^2}{T} D_t \left( \nabla_d^2 \Psi_d\right) = \nu \frac{1}{L^4} \frac{L^2}{T} \nabla_d^4 \Psi_d - g \alpha \frac{ \Delta T}{L} \frac{\partial \Theta_d}{\partial x_d} \]
\[ \frac{\Delta T}{T} D_t \Theta_d \quad = \frac{\Delta T}{H} \frac{L^2}{ T L} \frac{\partial \Psi_d}{\partial x_d} + \kappa \frac{\Delta T}{L^2} \nabla_d^2 \Theta_d \quad \]
\[ \mbox{Inserting} \quad T= H^2/\kappa \] \[ \mbox{Rayleigh number} \quad R_a = \frac{g \alpha H^3 \Delta T}{\nu \kappa} \] \[ \mbox{Prandtl number} \quad \sigma = \frac{ \nu}{ \kappa} \]
Non-dimensional Rayleigh-Benard system
\[ \frac{1}{T} \frac{1}{L^2} \frac{L^2}{T} D_t \left( \nabla_d^2 \Psi_d\right) = \nu \frac{1}{L^4} \frac{L^2}{T} \nabla_d^4 \Psi_d - g \alpha \frac{ \Delta T}{L} \frac{\partial \Theta_d}{\partial x_d} \]
\[ \frac{\Delta T}{T} D_t \Theta_d \quad = \frac{\Delta T}{H} \frac{L^2}{ T L} \frac{\partial \Psi_d}{\partial x_d} + \kappa \frac{\Delta T}{L^2} \nabla_d^2 \Theta_d \quad \]
\[ \mbox{Inserting} \quad T= H^2/\kappa \] \[ \mbox{Rayleigh number} \quad R_a = \frac{g \alpha H^3 \Delta T}{\nu \kappa} \] \[ \mbox{Prandtl number} \quad \sigma = \frac{ \nu}{ \kappa} \]
\[ D_t \left( \nabla_d^2 \Psi_d\right) = \sigma \nabla_d^4 \Psi_d - R_a \sigma \frac{\partial \Theta_d}{\partial x_d} \]
\[ D_t \Theta_d \quad = \frac{\partial \Psi_d}{\partial x_d} + \nabla_d^2 \Theta_d \quad \]
Galerkin approximation: Get a low-order model
\[ \mbox{ Saltzman (1962): Expand } \Psi, \Theta \mbox{ in double Fourier series in x and z: } \]
\[ \Psi (x,z,t) \, = \, \sum_{k=1}^\infty \sum_{l=1}^\infty \Psi_{k,l} (t) \, \, \sin \left(\frac{k \pi a}{H} x \right) \, \times \, \sin \left(\frac{ l \pi}{H} z \right) \] \[ \Theta (x,z,t) \, = \, \sum_{k=1}^\infty \sum_{l=1}^\infty \Theta_{k,l} (t) \cos \left(\frac{k \pi a}{H} x \right) \, \times \, \sin \left( \frac{l \pi}{H} z \right) \]
Approximation: Just 3 Modes X(t), Y(t), Z(t)
\[ \frac{a}{1+a^2} \, \kappa \, \Psi = X \sqrt{2} \sin\left(\frac{\pi a}{H} x \right) \sin\left(\frac{\pi}{H} z \right) \]
\[ \pi \frac{R_a}{R_c} \frac{1}{\Delta T} \, \Theta = Y \sqrt{2} \cos\left(\frac{\pi a}{H} x\right) \sin\left(\frac{\pi}{H} z \right) - Z \sin\left(2 \frac{\pi}{H} z \right) \]
Rayleigh number Ra: Buoyancy & Viscosity
\[ \mbox{Motion develops if } \quad R_a = \frac{g \alpha H^3 \Delta T}{\nu \kappa} \quad \mbox{exceeds } \quad R_c = \pi^4 \frac{(1+a^2)^3}{a^2} \]
\[ \mbox{The minimum value of $R_c = 657.51$ occurs when $a^2 = 1/2$. } \]
\[ \mbox{When } R_a < R_c,\mbox{ heat transfer is due to conduction} \]
\[ \mbox{When } R_a > R_c, \mbox{ heat transfer is due to convection.} \]

Lorenz system
Bifurcation at \[ r = R_a/R_c = 1 \]
Geometry constant \[ b = 4(1+a^2)^{-1} \]
Famous low-order model:
\[ \dot X = -\sigma X + \sigma Y \]
\[ \dot Y = r X - Y - X Z \]
\[ \dot Z = -b Z + X Y \]
\[ \mbox{dimensionless time } \quad t_d = \pi^2 H^{-2} (1+a^2) \kappa t, \]
\[ \mbox{ Prandtl number } \quad \sigma = \nu \kappa^{-1}, \]
Lorenz system r=24
r=24
s=10
b=8/3
dt=0.01
x=0.1
y=0.1
z=0.1
vx<-c(0)
vy<-c(0)
vz<-c(0)
for(i in 1:10000){
x1=x+s*(y-x)*dt
y1=y+(r*x-y-x*z)*dt
z1=z+(x*y-b*z)*dt
vx[i]=x1
vy[i]=y1
vz[i]=z1
x=x1
y=y1
z=z1}
plot(vx,vy,type="l",xlab="x",ylab="y")
plot(vy,vz,type="l",xlab="y",ylab="z")
Lorenz system r=0.9
r=0.9
s=10
b=8/3
dt=0.01
x=1.1
y=0.1
z=11.1
vx<-c(0)
vy<-c(0)
vz<-c(0)
for(i in 1:100){
x1=x+s*(y-x)*dt
y1=y+(r*x-y-x*z)*dt
z1=z+(x*y-b*z)*dt
vx[i]=x1
vy[i]=y1
vz[i]=z1
x=x1
y=y1
z=z1}
plot(vx,type="l",xlab="time",ylab="x")
plot(vy,type="l",xlab="time",ylab="y")
Lorenz system r=3.5
r=3.5
s=10
b=8/3
dt=0.01
x=1.1
y=0.1
z=11.1
vx<-c(0)
vy<-c(0)
vz<-c(0)
for(i in 1:1000){
x1=x+s*(y-x)*dt
y1=y+(r*x-y-x*z)*dt
z1=z+(x*y-b*z)*dt
vx[i]=x1
vy[i]=y1
vz[i]=z1
x=x1
y=y1
z=z1}
plot(vx,type="l",xlab="time",ylab="x")
plot(vy,type="l",xlab="time",ylab="y")