Dynamics II: lecture 4
Gerrit Lohmann date: May 3, 2021
Organization of
Lecture: May 3. (Monday), 14:00 Prof. Dr. Gerrit Lohmann
Tutorial: May 3. (Monday), ca. 15:30 Justus Contzen, Lars Ackermann
Time required for Sheet: 8 h
May 11, 14:00: Lecture (online G. Lohmann, 45 min)
zoom
Fourth lecture (link)
Content in the script: Angular momentum and Hadley Cell, Engery balance model,Wind-driven ocean circulation
After the lecture: Read the script about Atmosphere and Ocean Dynamics (Chapter 4 and 5)
Reading/learning (the sections with a star are voluntary). It might take 80 min.
Scaling of the momentum
The Coriolis effect is one of the dominating forces for the large-scale dynamics.
\[ \underbrace{\frac{\partial \mathbf{v}}{\partial t}}_{ U/T \sim 10^{-8} } + \underbrace{\mathbf{v} \cdot \nabla \mathbf{v}}_{ U^2/L \sim 10^{-8} }= {\underbrace{- \frac{1}{\rho} \nabla p}_{ \bf \delta P/(\rho L) \sim 10^{-5} } + \underbrace{2 \mathbf{\Omega \times v}}_{ \bf f_0 U \sim 10^{-5} } + \underbrace{fric}_{ \nu U/H^2 \sim 10^{-13}}} \quad \]
complemented by the dynamics for the vertical component
\[ \underbrace{\frac{\partial w}{\partial t}}_{ \begin{smallmatrix} W/T \sim 10^{-11} \end{smallmatrix}} + \underbrace{\mathbf{v} \cdot \nabla w}_{ UW/L \sim 10^{-11} } - \underbrace{\frac{u^2 + v^2 }{a}}_{ U^2/a \sim 10^{-9} } = \underbrace{ - \frac{1}{\rho} \frac{\partial p}{\partial z}}_{ \bf P_0/(\rho H) \sim 10} + \underbrace{ g }_{ \bf \sim 10} + \underbrace{f^{(2)} u}_{ \bf \sim 10^{-5}} + \underbrace{\nu \partial_z^2 w}_{ \nu W/H^2 \sim 10^{-16}} \]
In the coordinate system
\[ \frac{\partial u}{\partial t}+ \mathbf{v} \cdot \nabla u - \, \underbrace{ \frac{u v \tan \varphi }{a} - \frac{u w }{a}}_{\mbox{metric terms} } = - \frac{1}{\rho} \frac{\partial p}{\partial x} + f v - \, \underbrace{ f^{(2)} w}_{\mbox{small}} + \nu \nabla^2 u \]
\[ \frac{\partial v}{\partial t}+ \mathbf{v} \cdot \nabla v - \, \underbrace{ \frac{u^2 \tan \varphi }{a} - \frac{v w }{a}}_{\mbox{metric terms} } = - \frac{1}{\rho} \frac{\partial p}{\partial y} - f u + \nu \nabla^2 v \]
Example: Vorticity for a rigid body
\[ \nabla \times \boldsymbol{ u} = 2 \boldsymbol{ \Omega} \]
Example: Vorticity from shear at Cape Haterras
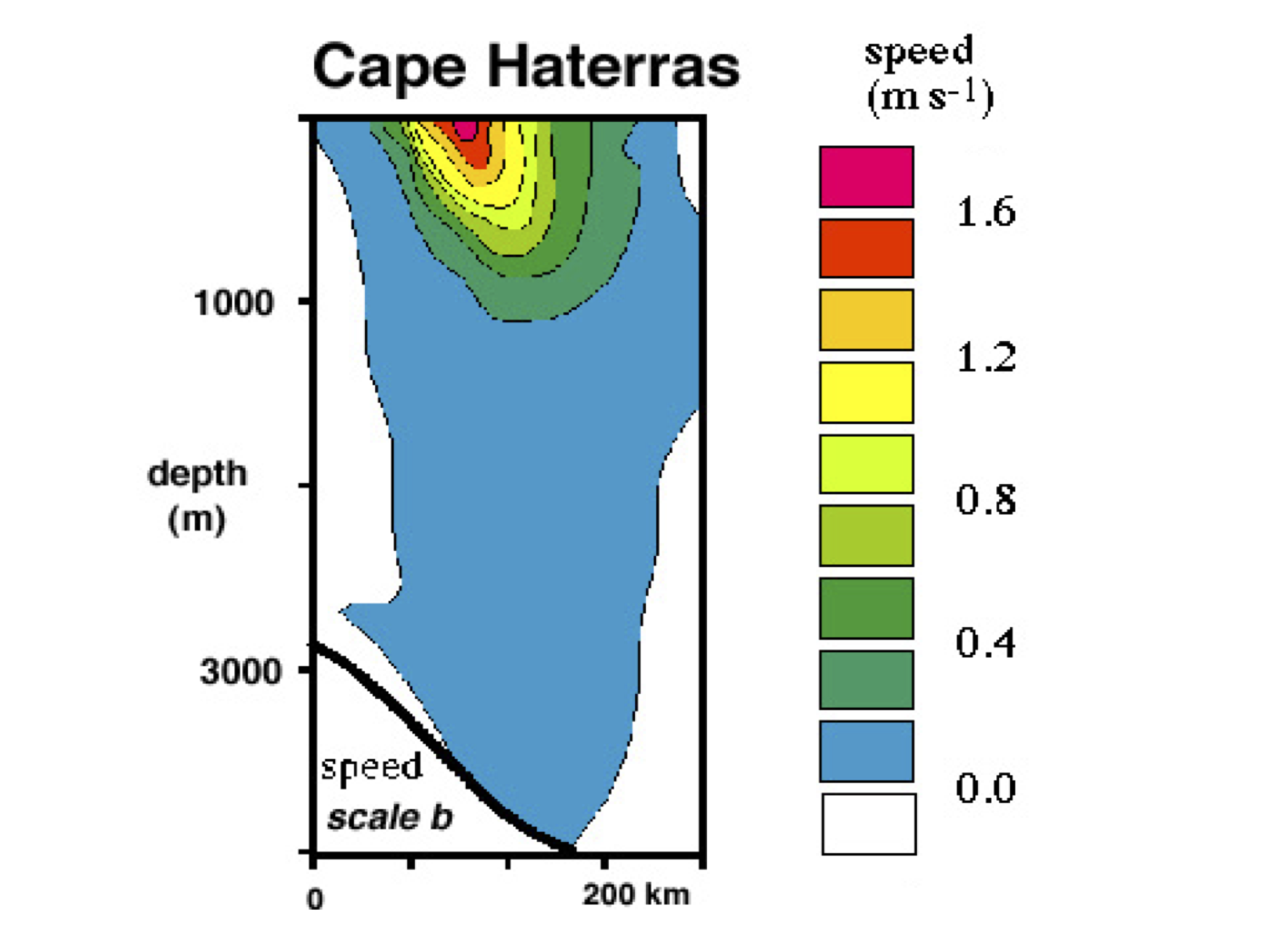
Tomczak & Godfrey
\[ u=0, v=v\left(x\right) \]
\[ \zeta= \partial v\left(x\right)/\partial x \]
Estimate for \( \zeta \) off Cape Hatteras:
the velocity changes by \( 1 \, {m}{s}^{-1} \) in 100 km
\[ \zeta= \frac{\partial v}{\partial x} = \frac{ 1 \, {m}{s}^{-1}}{100 \, {km}} = 10^{-5} \, \frac{1}{s} \]
still much smaller than
\[ f= 2 \Omega \sin \varphi = 2 \, \frac{2 \pi}{day} \sin \varphi \approx \, 10^{-4} \, \frac{1}{s} \]
Potential vorticity is conserved
\[ \frac{D}{Dt}\left(\zeta+f\right) + \left(\zeta + f\right)\left(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\right)=0 \quad \]
Couples depth, vorticity, latitude
– Changes in the depth results in change in \( \zeta \).
– Changes in latitude require a corresponding change in \( \zeta \).
Dietrich et al. (1980)
Ocean with depth h(x,y)
\[ \frac{D}{Dt}\left( \frac{\zeta+f}{h}\right) = 0 \quad \]
Steward, Oceanography
Conservation of Vorticity
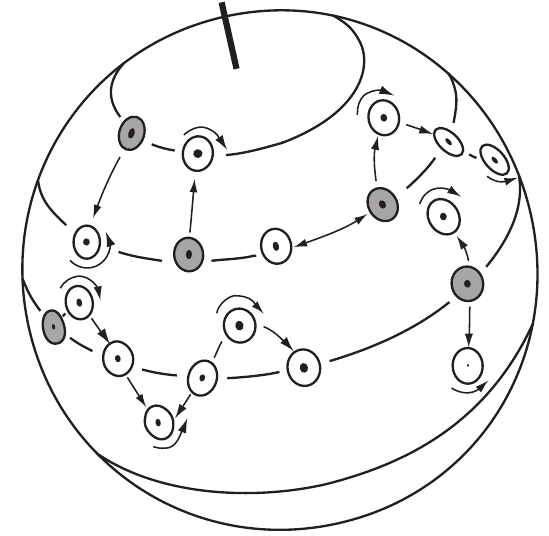
Vorticity tends to be conserved as columns of water change latitude. After von Arx (1962).
\[ \frac{D}{Dt}\left( \zeta+f\right) = 0 \]
If the barrel is moved southward, the water in it retains the rotation it had, and it will appear to rotate counterclockwise at the new latitude where f is smaller.
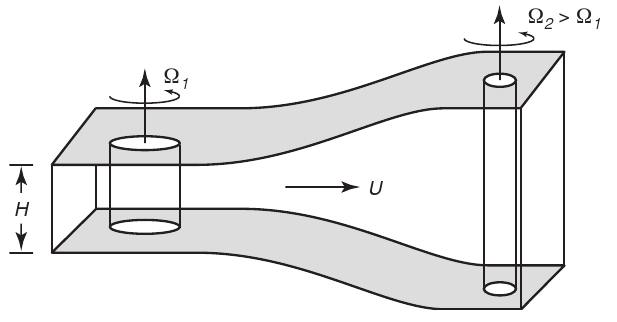
Taylor-Proudman Theorem
\[ \mbox{Assume constant density } \rho_0 \mbox{ on a plane with constant rotation } f=f_0 \neq 0 \]
\[ \frac{\partial v}{\partial z}=\frac{\partial u}{\partial z}=\frac{\partial v}{\partial z}=0 \]
Flow is two-dimensional and does not vary in the vertical direction.
Theorem applies to slowly varying flows.
Physical origin: stiffness endowed to the fluid by rapid rotation of the Earth.
Taylor's lab experiments: homogeneous fluid tends to move in vertical columns

Vertical velocity & north-south currents
Taylor-Proudman theorem: flow cannot expand or contract in the vertical
Assumption that \( f=f_0 \) can not be appropiate
\[ \quad \quad \quad \quad \frac{D}{Dt}\left(\zeta+f\right) + \left(\zeta + f\right)\left(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\right)=0 \quad \]
\[ \mbox{poor man's vorticity:} \quad \boxed{\beta\;v \quad + \quad f\left(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\right)= 0 } \quad \quad \quad \quad \]
Vertical velocity & north-south currents
Taylor-Proudman theorem: flow cannot expand or contract in the vertical
Assumption that \( f=f_0 \) can not be appropiate
\[ \quad \quad \quad \quad \frac{D}{Dt}\left(\zeta+f\right) + \left(\zeta + f\right)\left(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\right)=0 \quad \]
\[ \mbox{poor man's vorticity:} \quad \boxed{\beta\;v \quad + \quad f\left(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\right)= 0 } \quad \quad \quad \quad \]
Using the continuity equation, we obtain \[ \beta\;v = f \frac{\partial w_g}{\partial z} \] in the ocean's interior, geostrophic flow.
Variation of Coriolis force with latitude allows vertical velocity gradients in the interior of the ocean, and the vertical velocity leads to north-south currents.
Angular Momentum and Hadley Cell
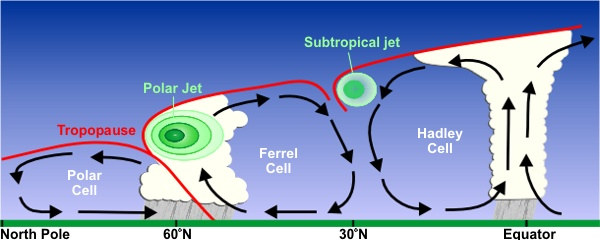
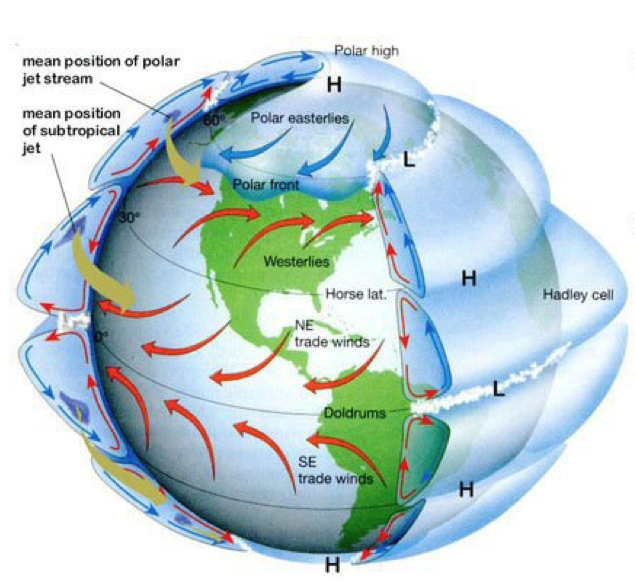
Tropical air rises to tropopause & moves poleward
Deflected eastward by the Coriolis force
Subtropical jet: forms at poleward limit of Hadley Cell
It tends to conserve angular momentum, friction small
equatorward moving air: westward component
Angular Momentum

Gyroscope remains upright while spinning due to conservation of its angular momentum
Magnitude of the angular momentum of an orbiting object:
momentum x perpendicular distance R from the rotation
1) Angular momentum of the Earth's orbit around the Sun
\[ m R \times u = m R^2 \omega = 5.97 \cdot 10^{24} \cdot \left(1.5\cdot 10^{11}\right)^2 \cdot \frac{2\pi}{365 \cdot 24 \cdot 3600} \]
2) Angular momentum of the Earth's spin
\[ =I \omega = \frac{2}{5} M R^2 \omega =\frac{2}{5} \cdot 5.97 \cdot 10^{24} \cdot \left(6.38 \cdot 10^6\right)^2 \cdot \frac{2\pi}{24 \cdot 3600} \]
Which is larger ?
Angular Momentum and Hadley Cell
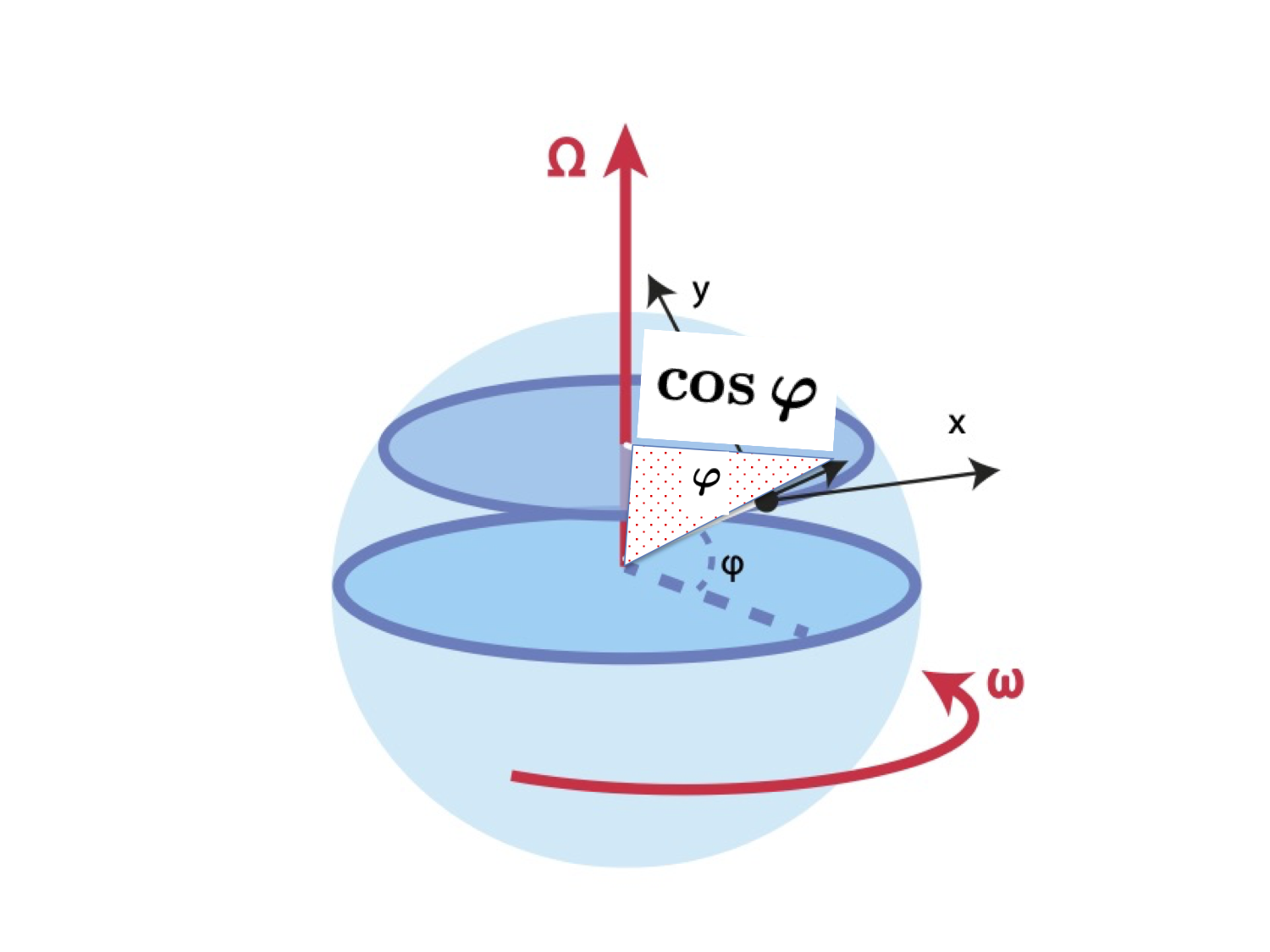
\( \Omega \) Earth rotation rate, \( u \) eastward wind
\( R= a \cos \varphi \) distance from rotation axis
\( U = R \Omega \) solid body speed
Absolute angular momentum per unit mass of fluid parcel (\( m^2/s \))
\[ \boldsymbol{ A }\quad= \quad \boldsymbol{ r } \quad \times \quad \boldsymbol{u_{tot} } \]
In the shallow troposphere \( r \approx a \) Earth radius
Angular momentum parallel to the Earth's rotation axis:
\[ A = R \, (U+u) = R \left( \Omega R + u \right) = \Omega a^{2} \cos^{2} \varphi + u a \cos \varphi \]
Angular Momentum and Hadley Cell

\( \Omega \) Earth rotation rate, \( u \) eastward wind
\( R= a \cos \varphi \) distance from rotation axis
\( U = R \Omega R \) solid body speed
Absolute angular momentum per unit mass of fluid parcel (\( m^2/s \))
\[ \boldsymbol{ A }\quad= \quad \boldsymbol{ r } \quad \times \quad \boldsymbol{u_{tot} } \]
In the shallow troposphere \( r \approx a \) Earth radius
Angular momentum parallel to the Earth's rotation axis:
\[ A = R \, (U+u) = R \left( \Omega R + u \right) = \Omega a^{2} \cos^{2} \varphi + u a \cos \varphi \]
In the inviscid upper troposphere, the flow conserves absolute angular momentum:
\[ \frac{DA}{Dt}=0 , \]
Angular Momentum and Hadley Cell
Consider a zonally symmetric circulation (no longitudinal variations).
a) Show, for inviscid zonally symmetric flow, that \( {DA}/{Dt}=0 \) is consistent with the zonal component of the equation of motion \[ \frac{Du}{Dt} - f v = -\frac{1}{\rho}\frac{\partial p}{\partial x} \]
Angular Momentum and Hadley Cell
Consider a zonally symmetric circulation (no longitudinal variations).
a) Show, for inviscid zonally symmetric flow, that \( {DA}/{Dt}=0 \) is consistent with the zonal component of the equation of motion \[ \frac{Du}{Dt} - f v = -\frac{1}{\rho}\frac{\partial p}{\partial x} \]
b) Use \( DA/dt=0 \) to describe how the existence of the Hadley Circulation explains the subtropical jet in the upper troposphere. Value of u at 20°N?
Angular Momentum and Hadley Cell
Consider a zonally symmetric circulation (no longitudinal variations).
a) Show, for inviscid zonally symmetric flow, that \( {DA}/{Dt}=0 \) is consistent with the zonal component of the equation of motion \[ \frac{Du}{Dt} - f v = -\frac{1}{\rho}\frac{\partial p}{\partial x} \]
b) Use \( DA/dt=0 \) to describe how the existence of the Hadley Circulation explains the subtropical jet in the upper troposphere. Value of u at 20°N?
c) Describe near-surface trade winds: low-level flow influenced by surface friction
Angular Momentum and Hadley Cell
Consider a zonally symmetric circulation (no longitudinal variations).
a) Show, for inviscid zonally symmetric flow, that \( {DA}/{Dt}=0 \) is consistent with the zonal component of the equation of motion \[ \frac{Du}{Dt} - f v = -\frac{1}{\rho}\frac{\partial p}{\partial x} \]
b) Use \( DA/dt=0 \) to describe how the existence of the Hadley Circulation explains the subtropical jet in the upper troposphere. Value of u at 20°N?
c) Describe near-surface trade winds: low-level flow influenced by surface friction
d) Hadley Circulation in northern winter:
Circulation rises at 10°S with u=0, sinks at 20°N. Calculate u at 0°, 10°N, 20°N !
a) Conservation of A, u-equation of motion
For inviscid axisymmetric flow, conservation of angular momentum implies \[ D_t (\Omega a^{2} \cos^{2} \varphi + u a \cos \varphi ) = 0 \]
Remember that \( y= a \varphi, dx = a \cos \varphi \, d \lambda \)
Here, we reformulate the planetary term: \[ D_t ( \Omega a^2 \cos^2 \varphi ) = v \partial_y ( \Omega a^2 \cos^2 \varphi ) = \Omega a v \partial_\varphi ( \cos^{2} \varphi ) \] \[ = -2 \Omega a v \sin \varphi \cos \varphi = -f v \cdot a \cos \varphi \]
a) Conservation of A, u-equation of motion
For inviscid axisymmetric flow, conservation of angular momentum implies \[ D_t (\Omega a^{2} \cos^{2} \varphi + u a \cos \varphi ) = 0 \]
Remember that \( y= a \varphi, dx = a \cos \varphi \, d \lambda \)
Here, we reformulate the planetary term: \[ D_t ( \Omega a^2 \cos^2 \varphi ) = v \partial_y ( \Omega a^2 \cos^2 \varphi ) = \Omega a v \partial_\varphi ( \cos^{2} \varphi ) \] \[ = -2 \Omega a v \sin \varphi \cos \varphi = -f v \cdot a \cos \varphi \] Similar \[ D_t (u a \cos \varphi ) = a \cos \varphi D_t u + u \cdot v \, \, \partial_\varphi \cos \varphi \] where in the coordinate system \[ D_t u = (\partial_t + u \partial_x + v \partial_y) u \, + \, \frac{uv}{a} \tan \varphi \] (the last term is a metric term). Therefore and under the assumption \( \partial_x p = 0 \): \[ D_t u -fv =0 \]
b) Conservation of A explains subtropical jet
\[ \mbox{At the equator } A_0 = \Omega a^2, \mbox{ flow rises from the ground there with no relative motion } \]
We have \[ A = \Omega a^{2} \cos^{2} \varphi + u a \cos \varphi = A_0 = \Omega a^2 \]
\[ u a \cos \varphi = \Omega a^2 ( 1 - \cos^{2} \varphi ) \]
\[ u = \Omega a \frac{\sin^2 \varphi}{ \cos \varphi } \]
The zonal flow u will be greatest at the edge of the cell, where \( \varphi \) is greatest, thus producing the subtropical jet.

b) Conservation of A explains subtropical jet
Assume the Hadley circulation is symmetric about the equator, and its edge is at 20°N, determine the strength of the subtropical jet by \[ u (20^\circ) = \Omega a \sin^{2} (20^\circ) / \cos (20^\circ) \, = \, \, \, 57.6 \, m \, s^{-1} \]
(The observed zonal winds are weaker than the value. In reality, non-axisymmetric atmospheric eddies act to reduce angular momentum strength of the jet.)

Solution c) about low-level return flow
flow is under the influence of surface friction: A will be progressively reduced:
\[ A_{low} < A_0 \]
\[ \Omega a^{2} \cos^{2}\varphi + u_{low} \, a \cos \varphi < \Omega a^2 \]
Solution c) about low-level return flow
flow is under the influence of surface friction: A will be progressively reduced:
\[ A_{low} < A_0 \]
\[ \Omega a^{2} \cos^{2}\varphi + u_{low} \, a \cos \varphi < \Omega a^2 \]
\[ \mbox{Thus} \quad u_{low} < \Omega a \frac{\sin^2 \varphi}{\cos \varphi} \]
\[ \mbox{ and some } \varphi_0 \mbox{ north of the equator that } u_{low} \mbox{ becomes negative (eastward winds), } \]
the low level flow will be equatorward and eastward there.
(Note that \( \Omega a^2 = \frac{2 \pi}{86400 \, s } \cdot (6.371 \cdot 10^6 m)^2 = 3 \cdot 10^9 m^2 s^{-1}. \))
d) Hadley Circulation in northern winter
Consider the angular momentum
\[ A = \Omega a^{2} \cos^{2} \varphi + u a \cos \varphi = A_0 \]
with
\[ \quad A_0 = \Omega a^2 \cos^{2} (10^\circ S) = 2.952 \cdot 10^9 m^2 s^{-1} \]
d) Hadley Circulation in northern winter
Consider the angular momentum
\[ A = \Omega a^{2} \cos^{2} \varphi + u a \cos \varphi = A_0 \]
with
\[ \quad A_0 = \Omega a^2 \cos^{2} (10^\circ S) = 2.952 \cdot 10^9 m^2 s^{-1} \]
\[ \mbox{Therefore} \quad u = \frac{A_0 - \Omega a^2 \cos^{2} \varphi }{ a \cos \varphi } \]
\[ \mbox{at } \varphi =0^\circ, u = -13.9 \, m/s \] \[ \mbox{at } \varphi =10^\circ N, u = 0 \, m/s \] \[ \mbox{at } \varphi =20^\circ N, u = 42.8 \, m/s \]
Engery balance model
in other lectures
in the script
may be in one exercise
What drives the ocean currents?
Friction: transfer of momentum from atmosphere to oceanic Ekman layer
Vorticity dynamics for the ocean and include the wind stress term
\[ D_t u - f v = - \frac{1}{\rho} \frac{\partial p}{\partial x} + \frac{1}{\rho} \partial_z \tau_{xz} \] \[ D_t v + f u = - \frac{1}{\rho} \frac{\partial p}{\partial y} + \frac{1}{\rho} \partial_z \tau_{yz} \]
What drives the ocean currents?
Friction: transfer of momentum from atmosphere to oceanic Ekman layer
Vorticity dynamics for the ocean and include the wind stress term
\[ D_t u - f v = - \frac{1}{\rho} \frac{\partial p}{\partial x} + \frac{1}{\rho} \partial_z \tau_{xz} \] \[ D_t v + f u = - \frac{1}{\rho} \frac{\partial p}{\partial y} + \frac{1}{\rho} \partial_z \tau_{yz} \]
\[ \frac{D}{Dt} \left( {\zeta+f}\right) - \frac{\left(\zeta+f \right)}{h} \frac{D}{Dt} h \, = \, \frac{1}{\rho} \underbrace{\left( \frac{\partial}{\partial x} \, \partial_z \tau_{yz} - \frac{\partial}{\partial y}\, \partial_z \tau_{xz} \right)}_{curl \, \partial_z \tau} \quad . \]
\[ \frac{D}{Dt} \left( \frac{\zeta+f}{h}\right) = \frac{1}{\rho \, h} \, \mbox{curl} \, \partial_z \tau \, \]
Sverdrup relation
\[ \frac{D}{Dt} \left( {\zeta+f}\right) - \frac{\left(\zeta+f \right)}{h} \frac{D}{Dt} h \, = \, \frac{1}{\rho} \underbrace{\left( \frac{\partial}{\partial x} \, \partial_z \tau_{yz} - \frac{\partial}{\partial y}\, \partial_z \tau_{xz} \right)}_{\operatorname{curl} \, \partial_z \tau} \quad . \]
Sverdrup relation
\[ \frac{D}{Dt} \left( {\zeta+f}\right) - \frac{\left(\zeta+f \right)}{h} \frac{D}{Dt} h \, = \, \frac{1}{\rho} \underbrace{\left( \frac{\partial}{\partial x} \, \partial_z \tau_{yz} - \frac{\partial}{\partial y}\, \partial_z \tau_{xz} \right)}_{\operatorname{curl} \, \partial_z \tau} \quad . \]
Assumption: h is constant, and poor man's vorticity
\[ v \beta = \frac{1}{\rho} \, \left( \frac{\partial}{\partial x} \, \partial_z \tau_{yz} - \frac{\partial}{\partial y}\, \partial_z \tau_{xz} \right) \quad . \]
Sverdrup relation
\[ \frac{D}{Dt} \left( {\zeta+f}\right) - \frac{\left(\zeta+f \right)}{h} \frac{D}{Dt} h \, = \, \frac{1}{\rho} \underbrace{\left( \frac{\partial}{\partial x} \, \partial_z \tau_{yz} - \frac{\partial}{\partial y}\, \partial_z \tau_{xz} \right)}_{\operatorname{curl} \, \partial_z \tau} \quad . \]
Assumption: h is constant, and poor man's vorticity
\[ v \beta = \frac{1}{\rho} \, \left( \frac{\partial}{\partial x} \, \partial_z \tau_{yz} - \frac{\partial}{\partial y}\, \partial_z \tau_{xz} \right) \quad . \]
Integrating over z, we receive \[ \beta \int_h^{0} dz \, v = \beta V = \frac{1}{\rho} \, \underbrace{\left( \frac{\partial \tau_{yz} }{\partial x} \, - \frac{\partial \tau_{xz}}{\partial y}\, \right)}_{\operatorname{curl} \, \tau} \]
Sverdrup transport
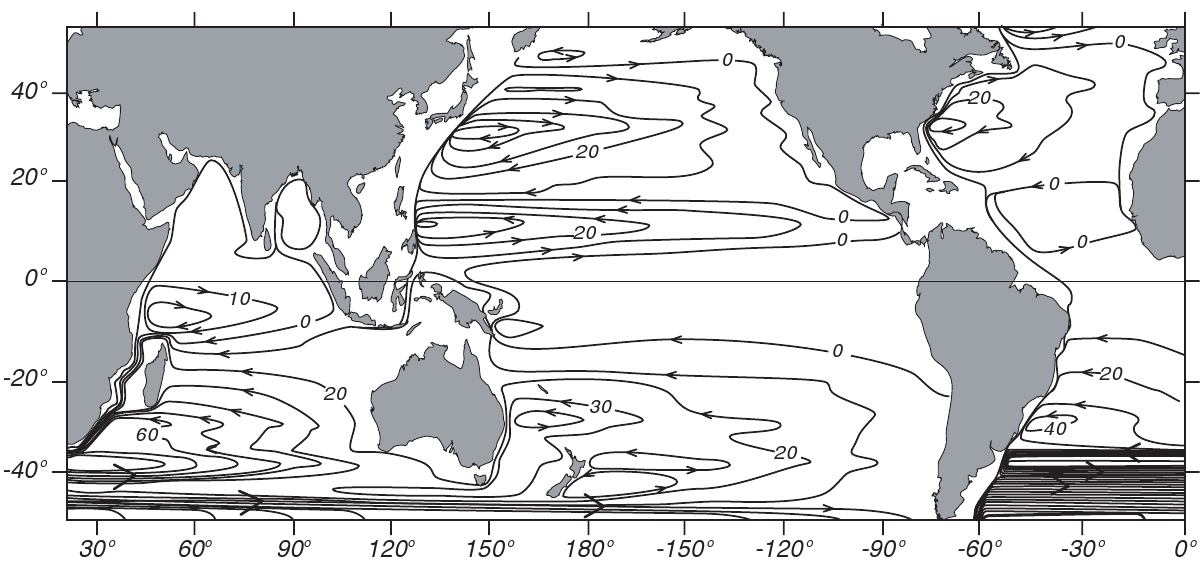
applied globally using the wind stress from Hellerman and Rosenstein (1983). Contour interval is \( 10 \) Sverdrups (Tomczak and Godfrey, 1994).
\[ V = \frac{1}{\rho \beta} \, \left( \frac{\partial \tau_{yz} }{\partial x} \, - \frac{\partial \tau_{xz}}{\partial y}\, \right) = \frac{1}{\rho \beta} \, \, \operatorname{curl} \, \tau \]
Ekman Pumping in a thin Ekman layer
The pressure terms are small because the Ekamn layer is thin (10-20 m)
The Ekman transports \( V_E, U_E \) describe the dynamics in the upper mixed layer: \[ f V_E = -{\tau_x/\rho} \ \] \[ f U_E = +{\tau_y/\rho} \] where \( U_E = \int_{-E}^0 u dz \) and \( V_E = \int_{-E}^0 v dz \)
depth-integrated velocities in the friction-dominated Ekman layer.
Ekman Pumping in a thin Ekman layer
The vertical velocity at the surface is zero and denote \( w_E \) as the Ekman vertical velocity the bottom of the Ekman layer. \[ - \int_{-E}^0 \frac{\partial w}{\partial z} dz = w_E = \frac{\partial}{\partial x} U_E + \frac{\partial}{\partial y} V_E \]
\( \operatorname{curl} \mathbf{\tau} \) produces a divergence of the Ekman transports leading to a vertical velocity \( w_E \) at the bottom of the Ekman layer.
\[ w_E = \, \frac{\partial }{\partial x} \left( \frac{ \tau_{y}}{\rho \;f }\, \right) - \frac{\partial }{\partial y}\, \left( \frac{ \tau_{x}}{\rho \;f }\, \right) =\operatorname{curl}\left(\frac{\mathbf{\tau}}{\rho\;f}\right) \simeq \frac{1}{\rho\;f} \, \operatorname{curl} \mathbf{\tau} \]
Ekman Pumping in a thin Ekman layer
The vertical velocity at the surface is zero and denote \( w_E \) as the Ekman vertical velocity the bottom of the Ekman layer. \[ - \int_{-E}^0 \frac{\partial w}{\partial z} dz = w_E = \frac{\partial}{\partial x} U_E + \frac{\partial}{\partial y} V_E \]
\( \operatorname{curl} \mathbf{\tau} \) produces a divergence of the Ekman transports leading to a vertical velocity \( w_E \) at the bottom of the Ekman layer.
\[ w_E = \, \frac{\partial }{\partial x} \left( \frac{ \tau_{y}}{\rho \;f }\, \right) - \frac{\partial }{\partial y}\, \left( \frac{ \tau_{x}}{\rho \;f }\, \right) =\operatorname{curl}\left(\frac{\mathbf{\tau}}{\rho\;f}\right) \simeq \frac{1}{\rho\;f} \, \operatorname{curl} \mathbf{\tau} \]
The order of magnitude of the Ekman vertical velocity:
typical wind stress variation of \( 0.2 N m^{-2} \) per 2000 km in y-direction:
\[ w_E \simeq - \frac{ \Delta \tau_{x}}{\rho \;f_0 \Delta y}\, \simeq \frac{1 }{10^3 kg m^{-3}} \frac{0.2 N m^{-2} }{10^{-4} s^{-1}\, \, 2 \cdot 10^6 m} \simeq 32 \, \, \frac{m}{yr} \]
Ekman Pumping & Sverdrup Transport
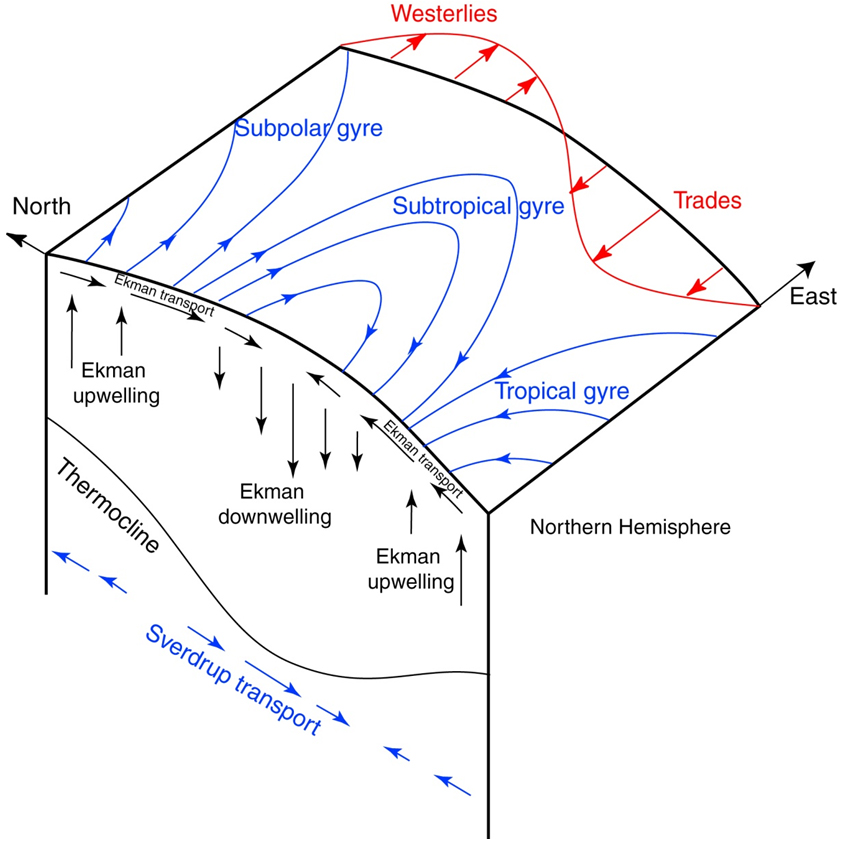
The center of a subtropical gyre is a high pressure zone: clockwise on the northern hemisphere.
Frictional surface currents towards the latitude at the center of the gyre.
This build-up of water in the center creates flow towards the equator.
is returned towards the pole in intensified western boundary currents: Gulf Stream, Kuroshio Currents
The Ekman vertical velocity balanced by \[ w_E=w_g \] vertical geostrophic current in the interior
Ekman vertical & vertical geostrophic velocities
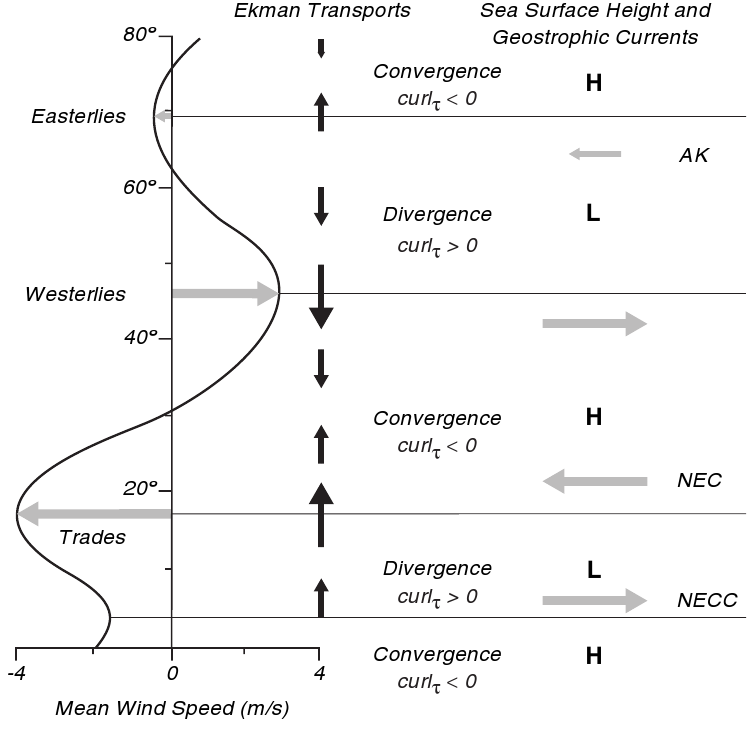
Mean zonal winds in the Pacific
Westerlies in the north drive a southward transport, the trades in the south drive a northward transport.
The converging Ekman transports must be balanced by downward geostrophic velocity
Ekman transports due to winds in the north Pacific lead to Ekman pumping, which sets up north-south pressure gradients in the upper ocean.
Horizontal lines: curl of the zonal wind stress changes sign. AK: Alaskan Current, NEC: North Equatorial Current, NECC: North Equatorial Counter Current.
Tea leaf paradox: Friction on the bottom matters
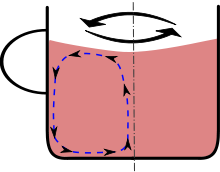
Observation:
tea leaves in a cup migrate to the center & bottom after being stirred rather than being forced to the edges of the cup, as would be expected in a spiral centrifuge.
Tea leaf paradox: Friction on the bottom matters

Observation:
tea leaves in a cup migrate to the center & bottom after being stirred rather than being forced to the edges of the cup, as would be expected in a spiral centrifuge.
Explanation:
Stirring the liquid makes it spin around the cup.
Pressure is higher along the rim than in the middle.
However, near the bottom and outer edges the liquid is slowed by the friction.
There the outward force cannot overcome the pressure gradient, so these pressure differences become more important for the water flow.
pressure gradient creates an inward flow along the bottom.
bringing the leaves to the center, then up, out and down near the rim. The leaves are too heavy to lift upwards, so they stay in the middle.
Low Pressure: Friction on the bottom matters

As the ground is approached from above, and the influence of friction becomes important, this balance changes. The friction slows down the primary circular motion, and thus the Coriolis force is lower and no longer sufficient for the fluid to flow parallel to the isobars.
There is a net inward force, and the air thus moves toward the center of the low, much like the tea leaves example.
Low Pressure: Friction on the bottom matters

As the ground is approached from above, and the influence of friction becomes important, this balance changes. The friction slows down the primary circular motion, and thus the Coriolis force is lower and no longer sufficient for the fluid to flow parallel to the isobars.
There is a net inward force, and the air thus moves toward the center of the low, much like the tea leaves example.
The converse case is also interesting. Around a high-pressure system, the air rotation is anticyclonic to achieve balance. In this case for the air outside the bottom boundary layer, the inward Coriolis force balances the outward radial pressure gradient.