Dynamics II: lecture 5
Gerrit Lohmann date: May 17, 2021
Organization of
Lecture: May 17. (Monday), 14:00 Prof. Dr. Gerrit Lohmann
Tutorial: May 17. (Monday), ca. 15:30 Justus Contzen, Lars Ackermann
Time required for Sheet 2: 8 h
May 17, 14:00: Lecture 5 (online G. Lohmann, 50 min)
klick here for the zoom session
5th lecture (link)
Read Chapter 11 (The thermohaline circulation of the ocean) in Marchal and Plumb
Reading/learning might take 90 min.
Fifth lecture (link to pdf will become available here)
Content in the script: Deep ocean circulation, Conceptual models
Potential vorticity is conserved
\[ \frac{D}{Dt}\left(\zeta+f\right) + \left(\zeta + f\right)\left(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\right)=0 \quad \]
Couples depth, vorticity, latitude
– Changes in the depth results in change in \( \zeta \).
– Changes in latitude require a corresponding change in \( \zeta \).
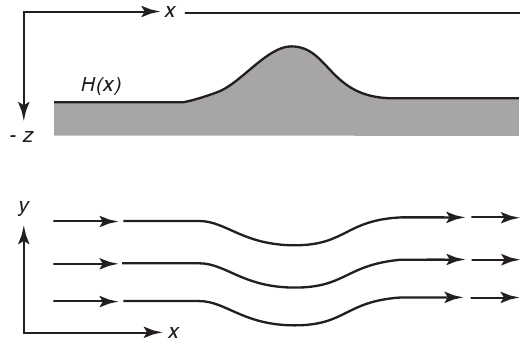
Dietrich et al. (1980)
Ocean with depth h(x,y)
\[ \frac{D}{Dt}\left( \frac{\zeta+f}{h}\right) = 0 \quad \]
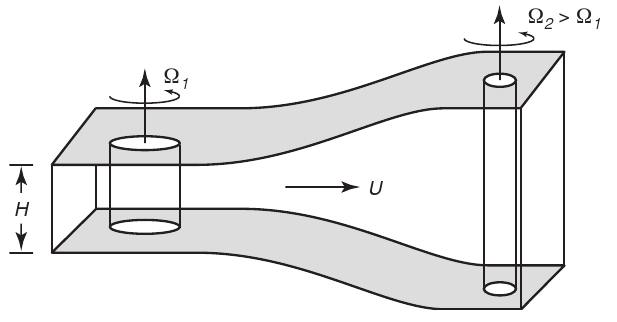
Steward, Oceanography
Angular Momentum and Hadley Cell
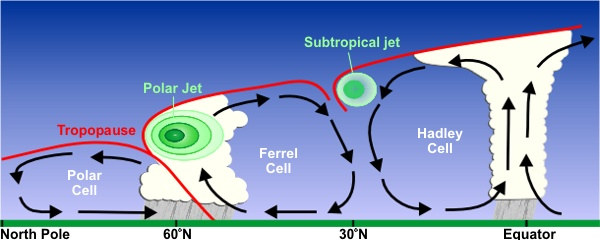
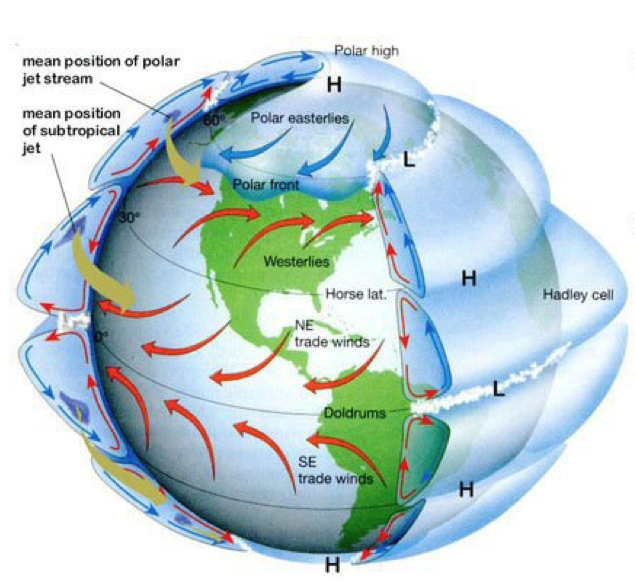
Tropical air rises to tropopause & moves poleward
Deflected eastward by the Coriolis force
Subtropical jet: forms at poleward limit of Hadley Cell
It tends to conserve angular momentum, friction small
equatorward moving air: westward component
Rotation and Hadley Cell
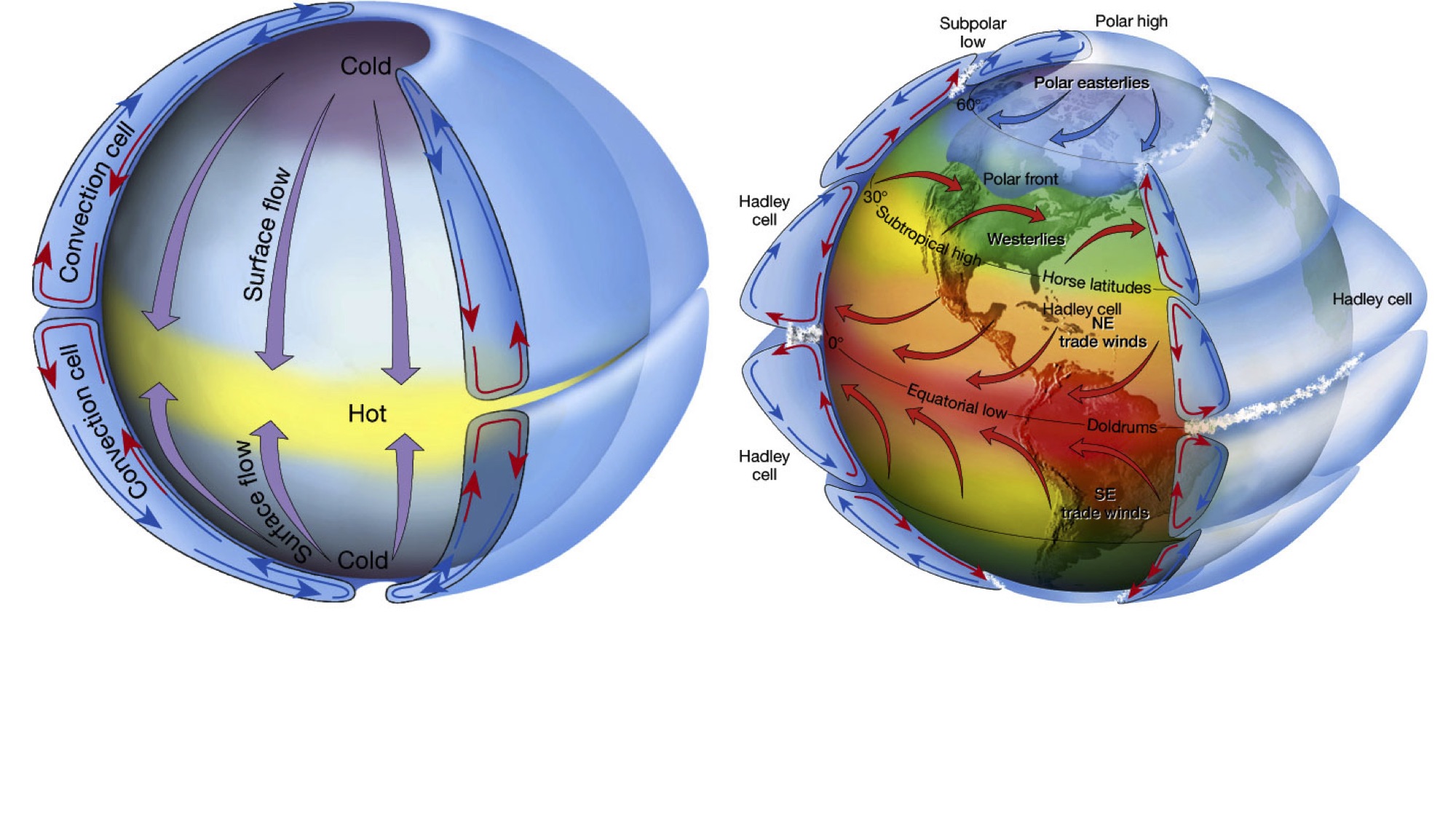
What drives the ocean currents?
Friction: transfer of momentum from atmosphere to oceanic Ekman layer
Vorticity dynamics for the ocean and include the wind stress term
\[ D_t u - f v = - \frac{1}{\rho} \frac{\partial p}{\partial x} + \frac{1}{\rho} \partial_z \tau_{xz} \] \[ D_t v + f u = - \frac{1}{\rho} \frac{\partial p}{\partial y} + \frac{1}{\rho} \partial_z \tau_{yz} \]
\[ \frac{D}{Dt} \left( {\zeta+f}\right) - \frac{\left(\zeta+f \right)}{h} \frac{D}{Dt} h \, = \, \frac{1}{\rho} \underbrace{\left( \frac{\partial}{\partial x} \, \partial_z \tau_{yz} - \frac{\partial}{\partial y}\, \partial_z \tau_{xz} \right)}_{curl \, \partial_z \tau} \quad . \]
\[ \frac{D}{Dt} \left( \frac{\zeta+f}{h}\right) = \frac{1}{\rho \, h} \, \mbox{curl} \, \partial_z \tau \, \]
Sverdrup transport
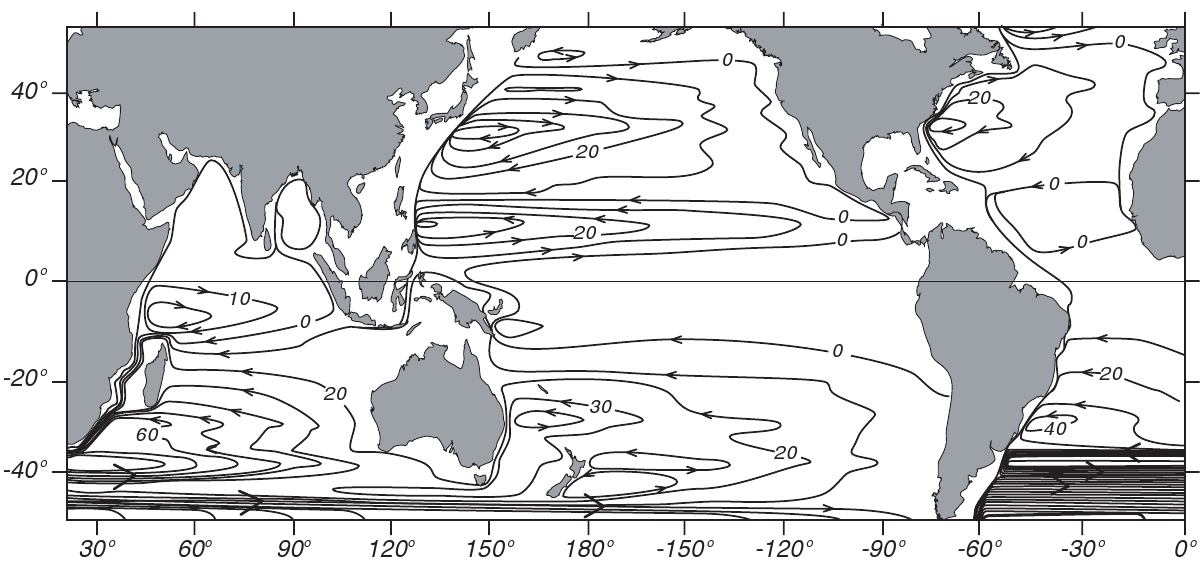
applied globally using the wind stress from Hellerman and Rosenstein (1983). Contour interval is \( 10 \) Sverdrups (Tomczak and Godfrey, 1994).
\[ V = \frac{1}{\rho \beta} \, \left( \frac{\partial \tau_{yz} }{\partial x} \, - \frac{\partial \tau_{xz}}{\partial y}\, \right) = \frac{1}{\rho \beta} \, \, \operatorname{curl} \, \tau \]
Ekman Pumping: vertical velocity at the bottom
\( w_E \) as the Ekman vertical velocity the bottom of the Ekman layer \[ w_E = - \int_{-E}^0 \frac{\partial w}{\partial z} dz = \frac{\partial}{\partial x} U_E + \frac{\partial}{\partial y} V_E \]
\( \operatorname{curl} \mathbf{\tau} \) produces a divergence of the Ekman transports leading to \( w_E \) at the bottom
\[ w_E = \, \frac{\partial }{\partial x} \left( \frac{ \tau_{y}}{\rho \;f }\, \right) - \frac{\partial }{\partial y}\, \left( \frac{ \tau_{x}}{\rho \;f }\, \right) =\operatorname{curl}\left(\frac{\mathbf{\tau}}{\rho\;f}\right) \simeq \frac{1}{\rho\;f} \, \operatorname{curl} \mathbf{\tau} \]
The order of magnitude of the Ekman vertical velocity:
typical wind stress variation of \( 0.2 N m^{-2} \) per 2000 km in y-direction:
\[ w_E \simeq - \frac{ \Delta \tau_{x}}{\rho \;f_0 \Delta y}\, \simeq \frac{1 }{10^3 kg m^{-3}} \frac{0.2 N m^{-2} }{10^{-4} s^{-1}\, \, 2 \cdot 10^6 m} \simeq 32 \, \, \frac{m}{yr} \]
Ekman Pumping & Sverdrup Transport
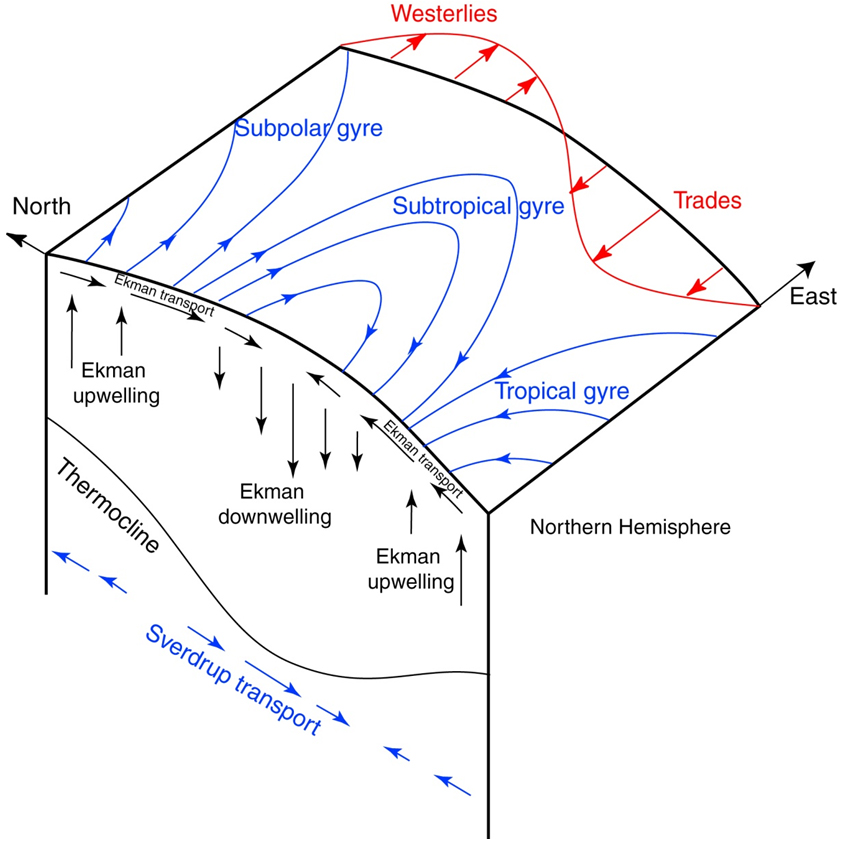
The center of a subtropical gyre is a high pressure zone: clockwise on the Northern Hemisphere
Ekman surface currents towards the center of the gyre
The Ekman vertical velocity balanced by \[ w_E=w_g \] vertical geostrophic current in the interior
geostrophic flow towards the equator
returned flow towards the pole in western boundary currents
North Atlantic Current & Gulfstream
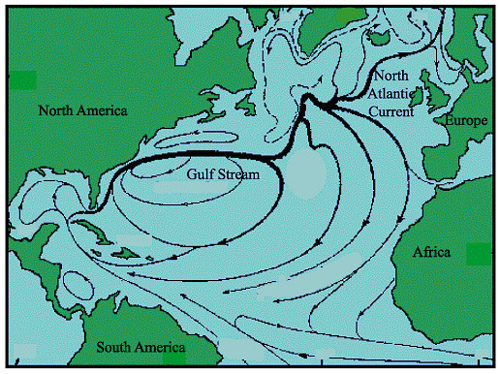
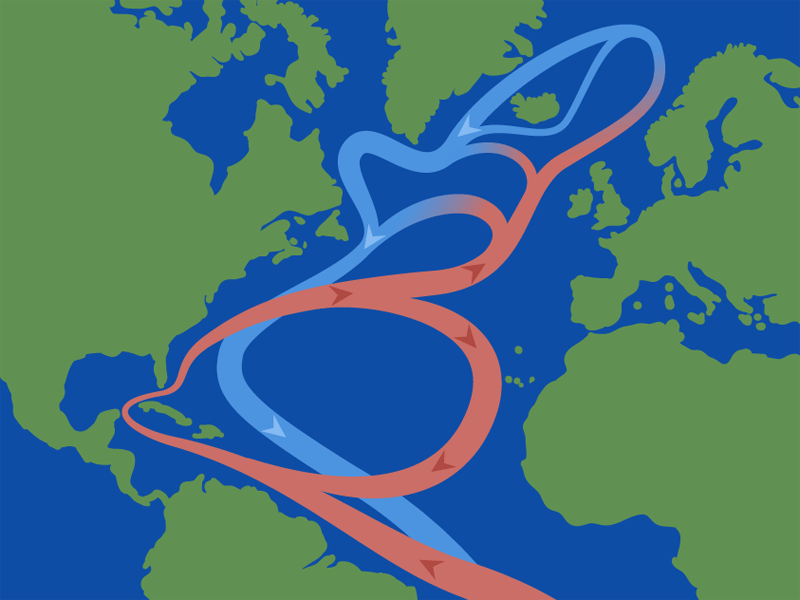
brings warm water northward where it cools.
returns southward as a cold, deep, western-boundary current.
Gulf Stream carries 40 Sv of 18°C water northward.
Of this, 15 Sv return southward in the deep western boundary current at a temperature of 2°C.
How much heat is transported northward ?
North Atlantic Current & Gulfstream


brings warm water northward where it cools.
returns southward as a cold, deep, western-boundary current.
Gulf Stream carries 40 Sv of 18°C water northward.
Of this, 15 Sv return southward in the deep western boundary current at a temperature of 2°C.
How much heat is transported northward ?
Calculation:
\[ \underbrace{ c_p}_{4.2 \cdot 10^3 Ws/(m^3 kg)} \, \cdot \, \underbrace{ \rho }_{10^3 kg/m^3 } \, \cdot \, \underbrace{\Phi}_{15 \cdot 10^6 m^3/s} \, \cdot \, \underbrace{\Delta T}_{(18-2) K } = 1 \cdot 10^{15} W \]
The flow carried by the conveyor belt loses 1 Petawatts (PW), close to estimates of Rintoul and Wunsch (1991)
North Atlantic Current & Gulfstream


brings warm water northward where it cools.
returns southward as a cold, deep, western-boundary current.
The deep bottom water from the North Atlantic is mixed upward in other regions and ocean, and it makes its way back to the Gulf Stream and the North Atlantic. Thus most of the water that sinks in the North Atlantic must be replaced by water from the far South Atlantic and Pacific Ocean.
Conveyor Belt
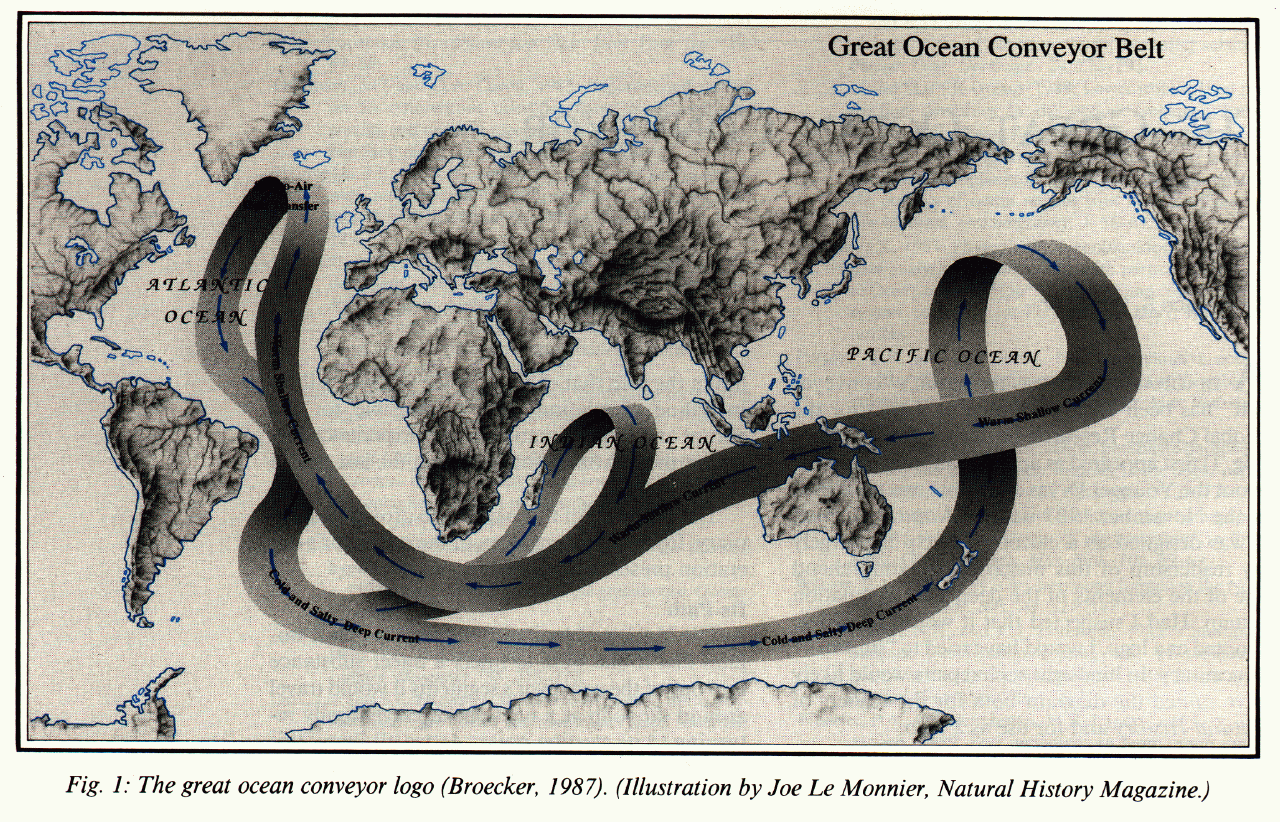
Conveyor Belt

Conveyor belt circulation
The the conveyor is driven by deepwater formation in the northern North Atlantic.
The conveyor belt metaphor necessarily simplifies the ocean system, it is of course not a full description of the deep ocean circulation.
Broecker's concept provides a successful approach for global ocean circulation, although several features can be wrong like the missing Antarctic bottom water, the upwelling areas etc..
metaphor inspired new ideas of halting or reversing the ocean circulation and put it into a global climate context.
interpretation of Greenland ice core records indicating different climate states with different ocean modes of operation (like on and off states of a mechanical maschine).
Thermohaline ocean circulation
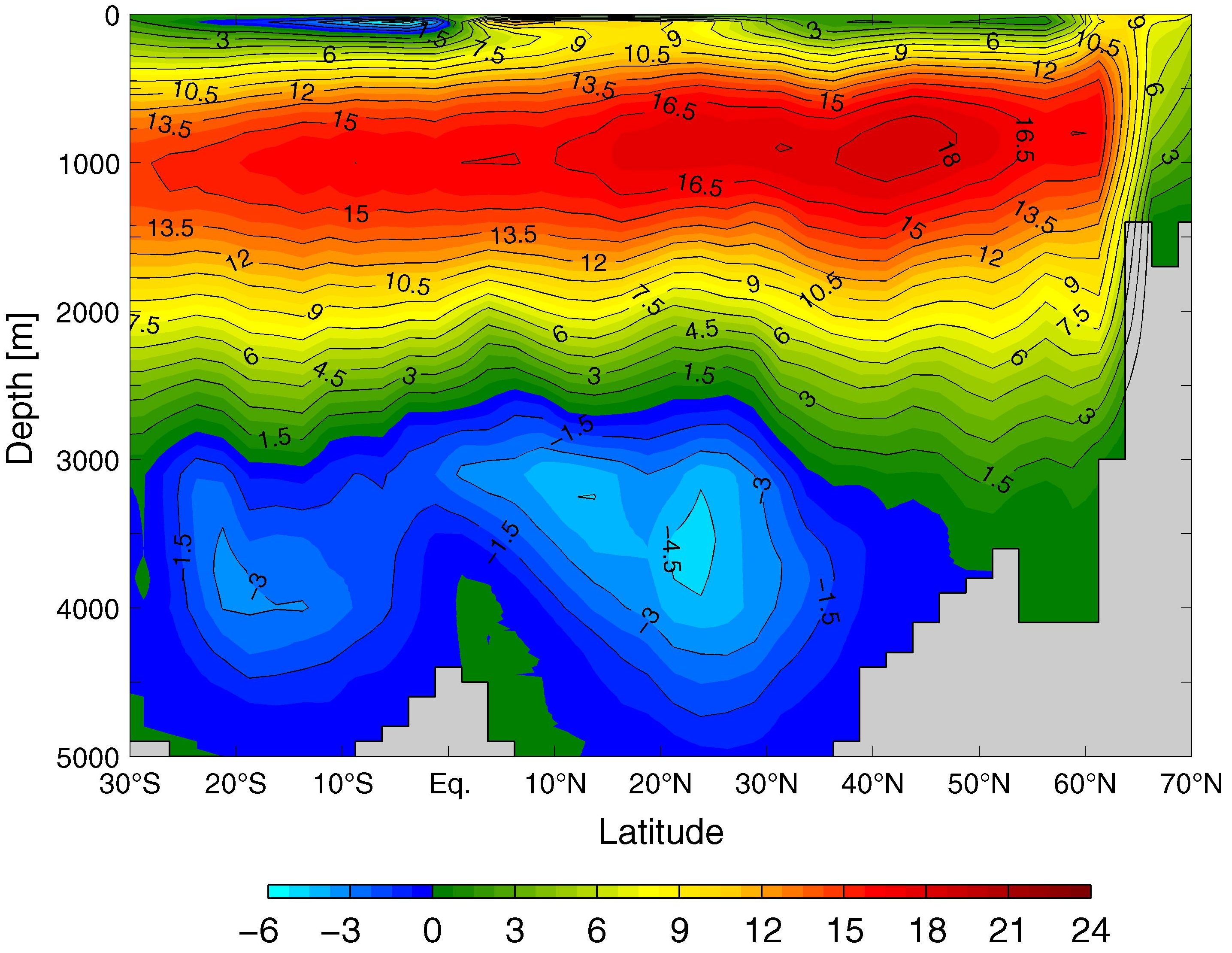 Modelled meridional overturning streamfunction in Sv 106 = m3 /s in the Atlantic Ocean. Grey areas represent zonally integrated smoothed bathymetry
Modelled meridional overturning streamfunction in Sv 106 = m3 /s in the Atlantic Ocean. Grey areas represent zonally integrated smoothed bathymetry
Meteor

Meteor Expedition, the first accurate hydrographic survey of the Atlantic from Wuest (1935).
Meteor

Meteor Expedition, the first accurate hydrographic survey of the Atlantic from Wuest (1935).
Meteor
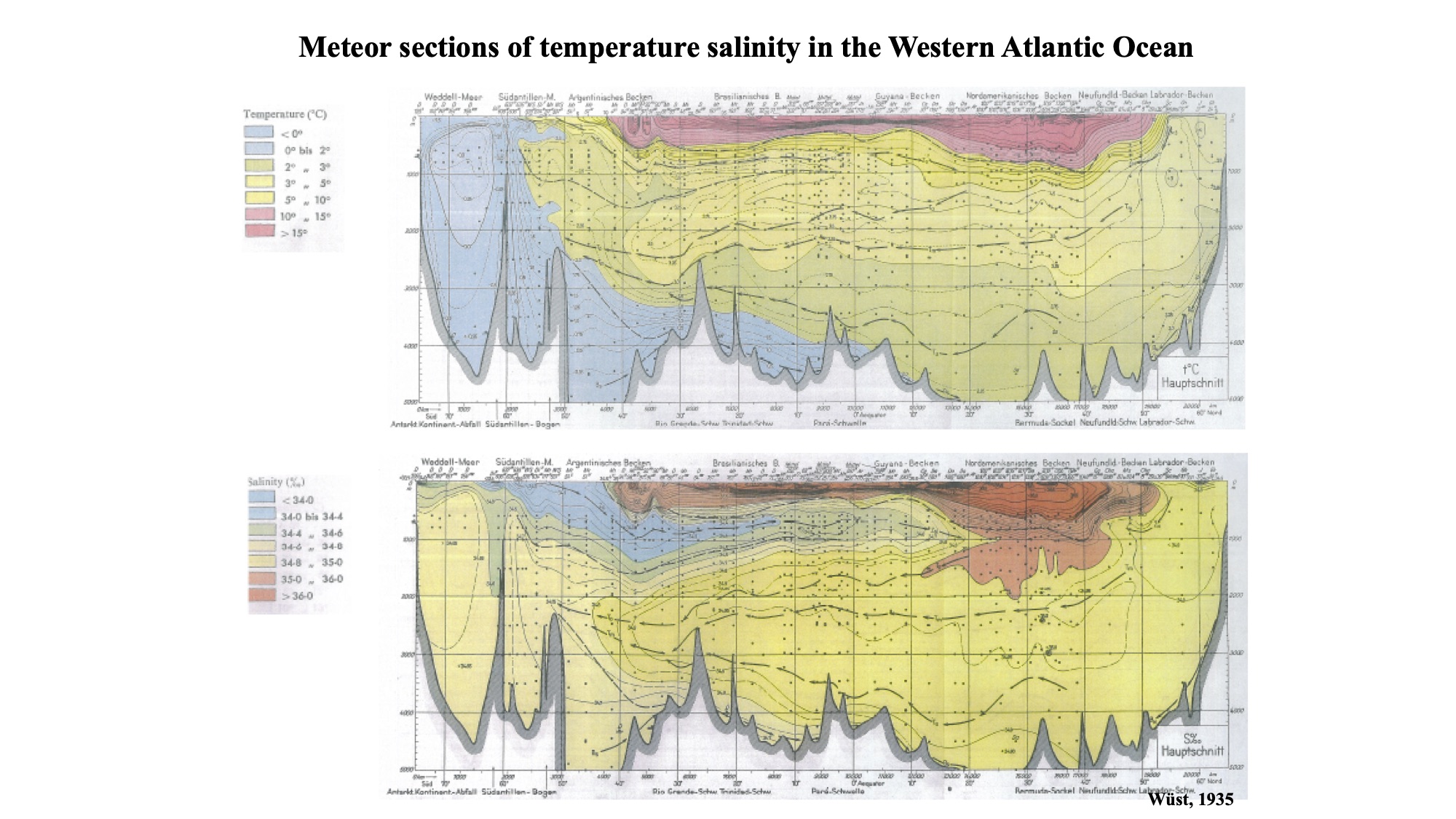
Lower panel: Salinity and dissolved oxygen on the Hauptschnitt along the western side of the Atlantic.
Estimates of overturning ?
It is observed that water sinks in to the deep ocean in polar regions of the Atlantic basin at a rate of 15 Sv. (Atlantic basin: 80,000,000 km2 area * 4 km depth.)
– How long would it take to 'fill up' the Atlantic basin?
– Supposing that the local sinking is balanced by large-scale upwelling, estimate the strength of this upwelling.
Hint: Upwelling = area * w
– Compare this number with that of the Ekman pumping!
Estimates of overturning
Timescale T to 'fill up' the Atlantic basin:
\[ T = \frac{ 80 \cdot 10^{12} \, m^2 \cdot 4000 \, m}{15 \cdot 10^6 \, m^3 s^{-1}} = 2.13 \cdot 10^{10} s = 676 \;years \]
Overturning is balanced by large-scale upwelling:
\[ area \cdot w = 15 \cdot 10^6 \, m^3 s^{-1} \]
\[ w = 0.1875 \cdot 10^{-6} m\;s^{-1} = 5.9 \cdot 10^{-15} m \; y^{-1}. \]
Ekman pumping \[ w_E \simeq 32 \, \, m \; y^{-1}. \]
Vorticity dynamics of meridional overturning (y,z)
\[ \frac{\partial}{\partial t} v \quad = \quad - \frac{1}{\rho_0} \frac{\partial p}{\partial y} \quad - \quad f u \quad - \quad \kappa v \]
\[ \frac{\partial}{\partial t} w \quad = \quad - \frac{1}{\rho_0} \frac{\partial p}{\partial z} \quad - \quad \frac{g}{\rho_0} (\rho -\rho_0) \quad - \quad \kappa w \] \( \kappa \) as parameter for Rayleigh friction.
Vorticity dynamics of meridional overturning (y,z)
\[ \frac{\partial}{\partial t} v \quad = \quad - \frac{1}{\rho_0} \frac{\partial p}{\partial y} \quad - \quad f u \quad - \quad \kappa v \]
\[ \frac{\partial}{\partial t} w \quad = \quad - \frac{1}{\rho_0} \frac{\partial p}{\partial z} \quad - \quad \frac{g}{\rho_0} (\rho -\rho_0) \quad - \quad \kappa w \] \( \kappa \) as parameter for Rayleigh friction.
Using the continuity equation
\[
0 \quad = \quad \frac{\partial v}{\partial y} \quad + \quad \frac{\partial w}{\partial z}
\]
\[ \mbox{ one can introduce a streamfunction } \Phi (y,z): v= \partial_z \Phi; w = - \partial_y \Phi \]
The associated vorticity equation in the (y,z)-plane is therefore
\[ \frac{\partial}{\partial t} \nabla^2 \Phi \, = \, - f \frac{\partial u}{\partial z} \quad + \quad \frac{g}{\rho_0} \frac{\partial \rho}{\partial y} \quad - \quad \kappa \nabla^2 \Phi \]
Galerkin approximation
\[ {\frac{\partial}{\partial t} \nabla^2 \Phi} \, = \, \underbrace{- f \frac{\partial u}{\partial z}}_{2.} \quad + \quad { \frac{g}{\rho_0} \frac{\partial \rho}{\partial y}} \quad - \quad \underbrace{ \kappa \nabla^2 \Phi }_{4.} \]
Term 2. is absorbed into the viscous term (4.)
\[ \Phi (y,z,t) \, = \, \sum_{k=1}^\infty \sum_{l=1}^\infty \Phi_{max}^{k,l} (t) \, \, \sin (\pi k y/L) \, \times \, \sin (\pi l z/H) \] yielding a first order differential equation in time for \( \Phi_{max}^{k,l} (t) \).
Simple ansatz satisfying that the normal velocity at the boundary vanishes \[ \Phi (y,z,t) \, = \, \Phi_{max} (t) \, \, \sin \left(\frac{\pi y}{L}\right) \, \times \, \sin \left(\frac{\pi z}{H}\right) \]
L and H dentote the meridional and depth extend: y from 0 to L, z from 0 to H
The remaining terms and integration
\[ \underbrace{\int_0^L dy \int_0^H dz \quad \frac{\partial}{\partial t} \nabla^2 \Phi}_{1.} \, = \, \underbrace{ \int_0^L dy \int_0^H dz \quad \frac{g}{\rho_0} \frac{\partial \rho}{\partial y}}_{2.} \quad - \underbrace{ \int_0^L dy \int_0^H dz \quad \kappa \nabla^2 \Phi }_{3.} \]
1. \[ \frac{d}{dt} \Phi_{max} \left(\frac{\pi^2}{L^2} + \frac{\pi^2}{H^2}\right) \int\limits_0^L dy \sin \left(\frac{\pi y}{L}\right) \int\limits_0^H dz \sin \left(\frac{\pi z}{H}\right) = 4 LH \left(\frac{1}{L^2} + \frac{1}{H^2}\right) \frac{d}{dt} \Phi_{max} \]
The remaining terms and integration
\[ \underbrace{\int_0^L dy \int_0^H dz \quad \frac{\partial}{\partial t} \nabla^2 \Phi}_{1.} \, = \, \underbrace{ \int_0^L dy \int_0^H dz \quad \frac{g}{\rho_0} \frac{\partial \rho}{\partial y}}_{2.} \quad - \underbrace{ \int_0^L dy \int_0^H dz \quad \kappa \nabla^2 \Phi }_{3.} \]
1. \[ \frac{d}{dt} \Phi_{max} \left(\frac{\pi^2}{L^2} + \frac{\pi^2}{H^2}\right) \int\limits_0^L dy \sin \left(\frac{\pi y}{L}\right) \int\limits_0^H dz \sin \left(\frac{\pi z}{H}\right) = 4 LH \left(\frac{1}{L^2} + \frac{1}{H^2}\right) \frac{d}{dt} \Phi_{max} \]
2. \[ \int\limits_0^L dy \int\limits_0^H dz \frac{g}{\rho_0} \frac{\partial \rho}{\partial y} = \frac{g}{\rho_0} \, H \, (\rho_{north} - \rho_{south}) \quad \mbox{ with } \rho_{north} = \rho (y=L) , \rho_{south} = \rho (y=0) \]
\[ \underbrace{\int_0^L dy \int_0^H dz \quad \frac{\partial}{\partial t} \nabla^2 \Phi}_{1.} \, = \, \underbrace{ \int_0^L dy \int_0^H dz \quad \frac{g}{\rho_0} \frac{\partial \rho}{\partial y}}_{2.} \quad - \underbrace{ \int_0^L dy \int_0^H dz \quad \kappa \nabla^2 \Phi }_{3.} \]
1. \[ \frac{d}{dt} \Phi_{max} \left(\frac{\pi^2}{L^2} + \frac{\pi^2}{H^2}\right) \int\limits_0^L dy \sin \left(\frac{\pi y}{L}\right) \int\limits_0^H dz \sin \left(\frac{\pi z}{H}\right) = 4 LH \left(\frac{1}{L^2} + \frac{1}{H^2}\right) \frac{d}{dt} \Phi_{max} \]
2. \[ \int\limits_0^L dy \int\limits_0^H dz \frac{g}{\rho_0} \frac{\partial \rho}{\partial y} = \frac{g}{\rho_0} \, H \, (\rho_{north} - \rho_{south}) \quad \mbox{ with } \rho_{north} = \rho (y=L) , \rho_{south} = \rho (y=0) \]
3. \[ \kappa \Phi_{max} \left(\frac{\pi^2}{L^2} + \frac{\pi^2}{H^2}\right) \int\limits_0^L dy \sin \left(\frac{\pi y}{L}\right) \int\limits_0^H dz \sin \left(\frac{\pi z}{H}\right) = \kappa \, 4 LH \left(\frac{1}{L^2} + \frac{1}{H^2}\right) \Phi_{max} \]
Amplitude of overturning
\[ \frac{d}{dt} \Phi_{max} \, = \, \frac{a}{\rho_0} (\rho_{north} - \rho_{south}) \, \, - \, \, \kappa \Phi_{max} \] with \[ a = g L H^2/4(L^2 + H^2) \, \]
This shows that the overturning circulation depends on the density differences on the right and left boxes.
It is simplified to a diagnostic relation
\[ \Phi_{max} = \frac{a}{\rho_0 \, \kappa} \, \, (\rho_{north} - \rho_{south}) \quad \]
because the adjustment of \( \Phi_{max} \) is quasi-instantaneous due to adjustment processes, e.g. Kelvin waves.
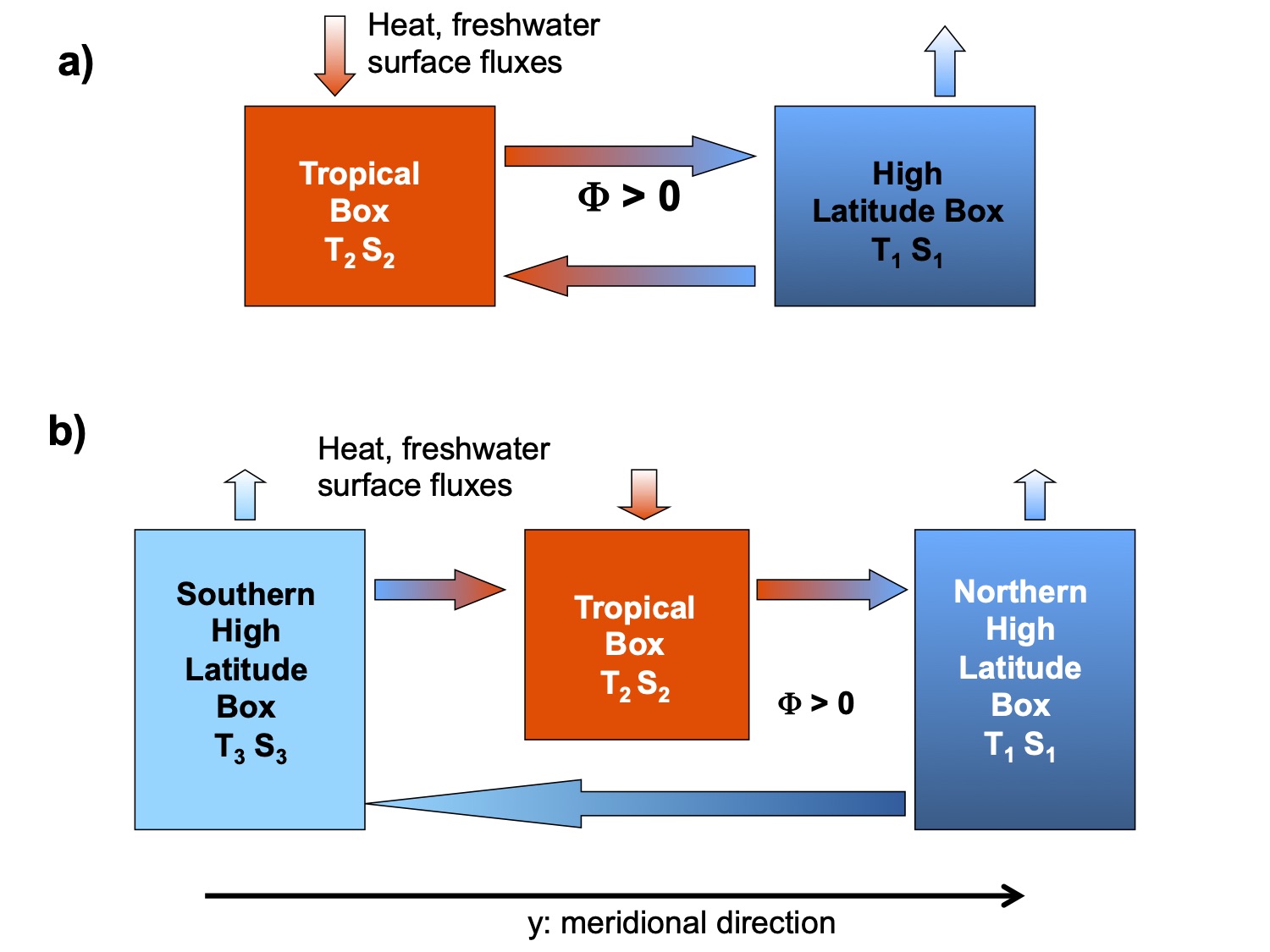
Schematic picture of the hemispheric two box model (a) and of the interhemispheric box model
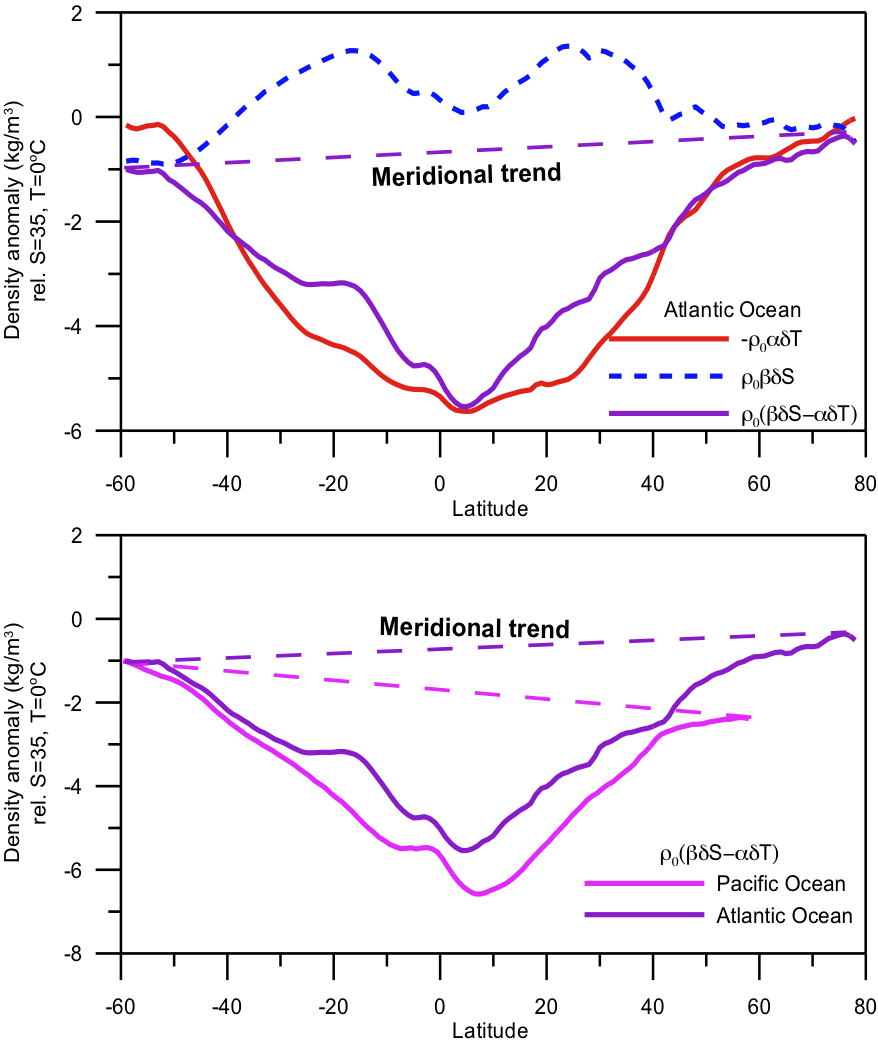
a) The Atlantic surface density is mainly related to temperature differences. b) But the pole-to-pole differences are caused by salinity differences. }