Dynamics II: lecture 6
Gerrit Lohmann date: May 31, 2021
Organization of
Lecture: May 31 (Monday), 14:00 Prof. Dr. Gerrit Lohmann
Tutorial: June 31 (Monday), ca. 15:30
Time required for Sheet 2: 8 h
Read Chapter 11 (The thermohaline circulation of the ocean) in Marchal and Plumb
Reading/learning might take 90 min.
6th lecture link
Content in the script: Deep ocean circulation, Conceptual models
What drives the ocean currents?
Friction: transfer of momentum from atmosphere to oceanic Ekman layer
Vorticity dynamics for the ocean and include the wind stress term
\[ D_t u - f v = - \frac{1}{\rho} \frac{\partial p}{\partial x} + \frac{1}{\rho} \partial_z \tau_{xz} \] \[ D_t v + f u = - \frac{1}{\rho} \frac{\partial p}{\partial y} + \frac{1}{\rho} \partial_z \tau_{yz} \]
\[ \frac{D}{Dt} \left( {\zeta+f}\right) - \frac{\left(\zeta+f \right)}{h} \frac{D}{Dt} h \, = \, \frac{1}{\rho} \underbrace{\left( \frac{\partial}{\partial x} \, \partial_z \tau_{yz} - \frac{\partial}{\partial y}\, \partial_z \tau_{xz} \right)}_{curl \, \partial_z \tau} \quad . \]
\[ \frac{D}{Dt} \left( \frac{\zeta+f}{h}\right) = \frac{1}{\rho \, h} \, \mbox{curl} \, \partial_z \tau \, \]
Sverdrup transport
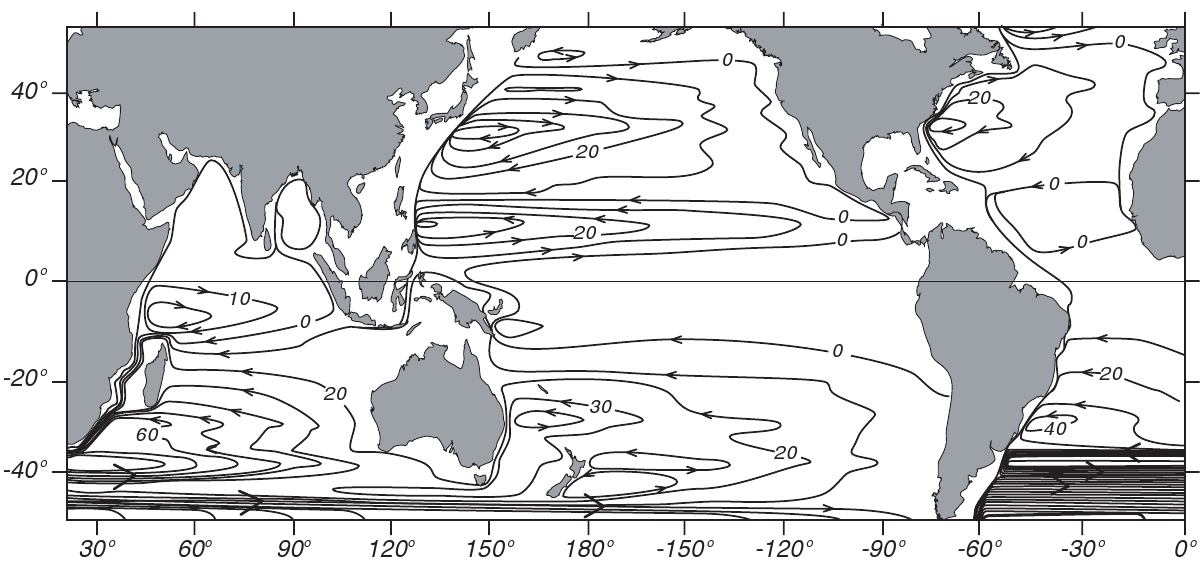
applied globally using the wind stress from Hellerman and Rosenstein (1983). Contour interval is \( 10 \) Sverdrups (Tomczak and Godfrey, 1994).
\[ V = \frac{1}{\rho \beta} \, \left( \frac{\partial \tau_{yz} }{\partial x} \, - \frac{\partial \tau_{xz}}{\partial y}\, \right) = \frac{1}{\rho \beta} \, \, \operatorname{curl} \, \tau \]
Ekman Pumping: vertical velocity at the bottom
\( w_E \) as the Ekman vertical velocity the bottom of the Ekman layer \[ w_E = - \int_{-E}^0 \frac{\partial w}{\partial z} dz = \frac{\partial}{\partial x} U_E + \frac{\partial}{\partial y} V_E \]
\( \operatorname{curl} \mathbf{\tau} \) produces a divergence of the Ekman transports leading to \( w_E \)
\[ w_E = \, \frac{\partial }{\partial x} \left( \frac{ \tau_{y}}{\rho \;f }\, \right) - \frac{\partial }{\partial y}\, \left( \frac{ \tau_{x}}{\rho \;f }\, \right) =\operatorname{curl}\left(\frac{\mathbf{\tau}}{\rho\;f}\right) \simeq \frac{1}{\rho\;f} \, \operatorname{curl} \mathbf{\tau} \]
The order of magnitude of the Ekman vertical velocity:
typical wind stress variation of \( 0.2 N m^{-2} \) per 2000 km in y-direction:
\[ w_E \simeq - \frac{ \Delta \tau_{x}}{\rho \;f_0 \Delta y}\, \simeq \frac{1 }{10^3 kg m^{-3}} \frac{0.2 N m^{-2} }{10^{-4} s^{-1}\, \, 2 \cdot 10^6 m} \simeq 32 \, \, \frac{m}{yr} \]
Ekman Pumping & Sverdrup Transport
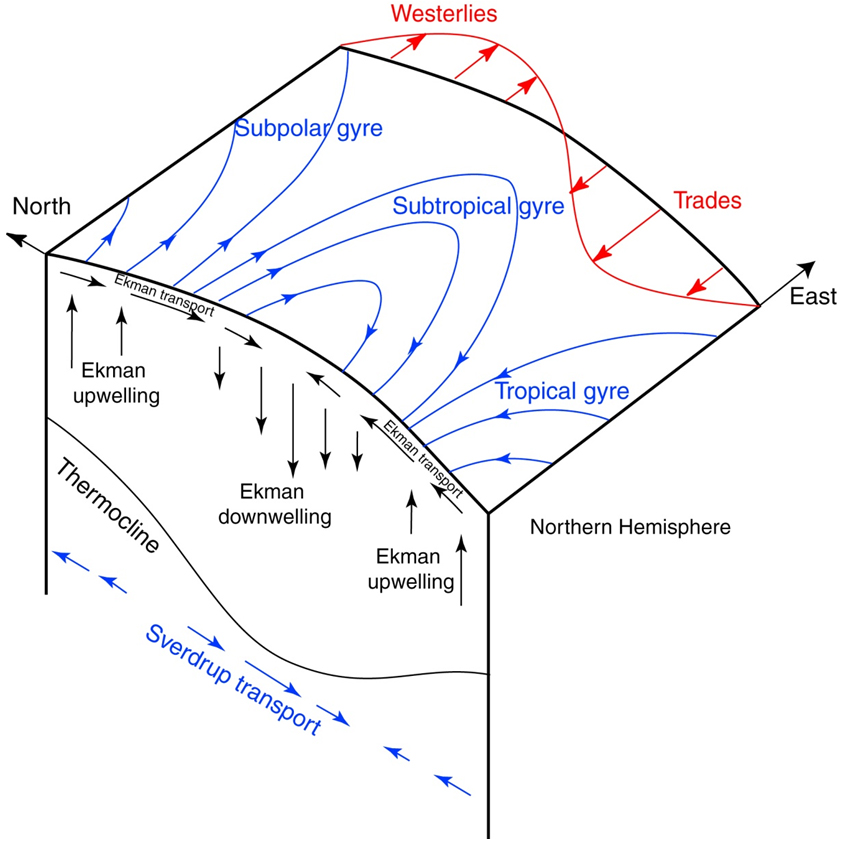
The center of a subtropical gyre is a high pressure zone: clockwise on the Northern Hemisphere
Ekman surface currents towards the center of the gyre
The Ekman vertical velocity balanced by \[ w_E=w_g \] vertical geostrophic current in the interior
geostrophic flow towards the equator
returned flow towards the pole in western boundary currents
Ocean layers
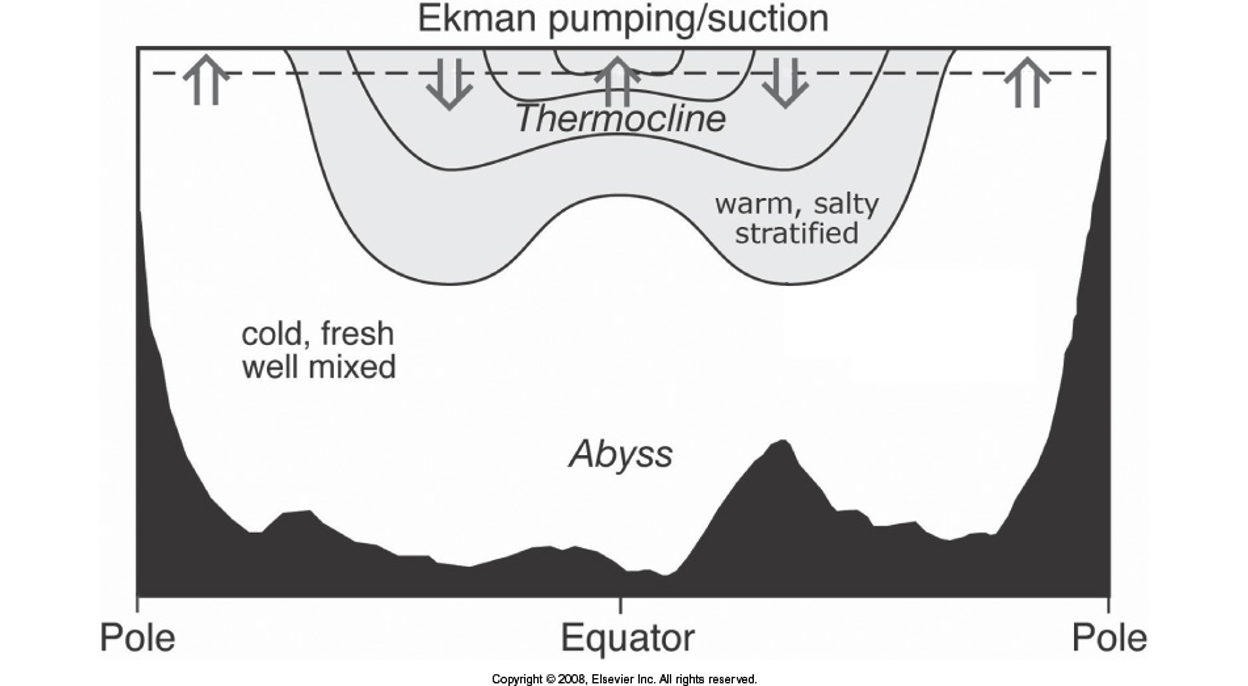
Steady winds blowing on the sea surface produce a thin, horizontal boundary layer, the Ekman layer. A similar boundary layer exists at the bottom of the atmosphere just above the sea surface, the planetary boundary layer.
North Atlantic Current & Gulfstream
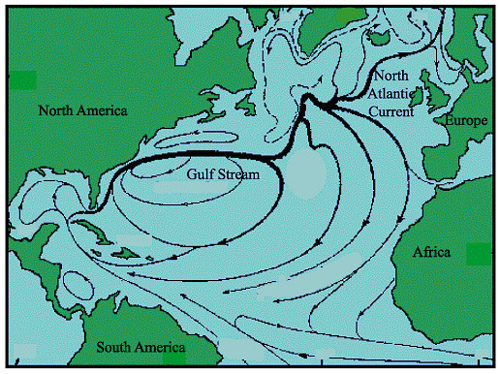
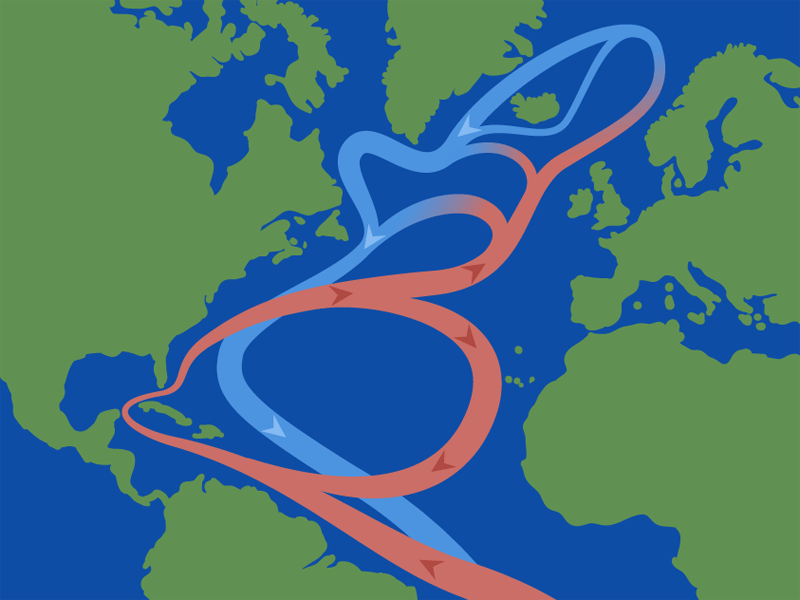
brings warm water northward where it cools.
returns southward as a cold, deep, western-boundary current.
Gulf Stream carries 40 Sv of 18°C water northward.
Of this, 15 Sv return southward in the deep western boundary current at a temperature of 2°C.
How much heat is transported northward ?
Calculation:
\[ \underbrace{ c_p}_{4.2 \cdot 10^3 Ws/(m^3 kg)} \, \cdot \, \underbrace{ \rho }_{10^3 kg/m^3 } \, \cdot \, \underbrace{\Phi}_{15 \cdot 10^6 m^3/s} \, \cdot \, \underbrace{\Delta T}_{(18-2) K } = 1 \cdot 10^{15} W \]
The flow carried by the conveyor belt loses 1 Petawatts (PW), close to estimates of Rintoul and Wunsch (1991)
Ocean heat transport
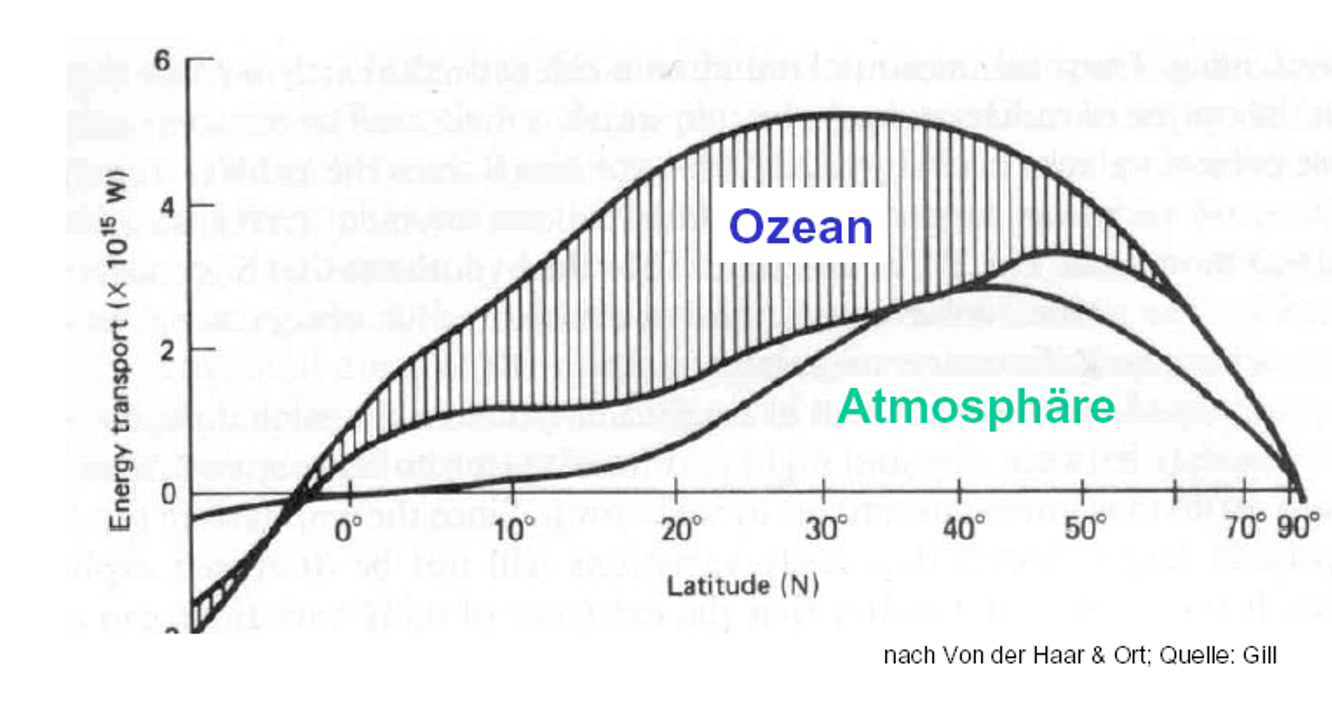
Conveyor Belt
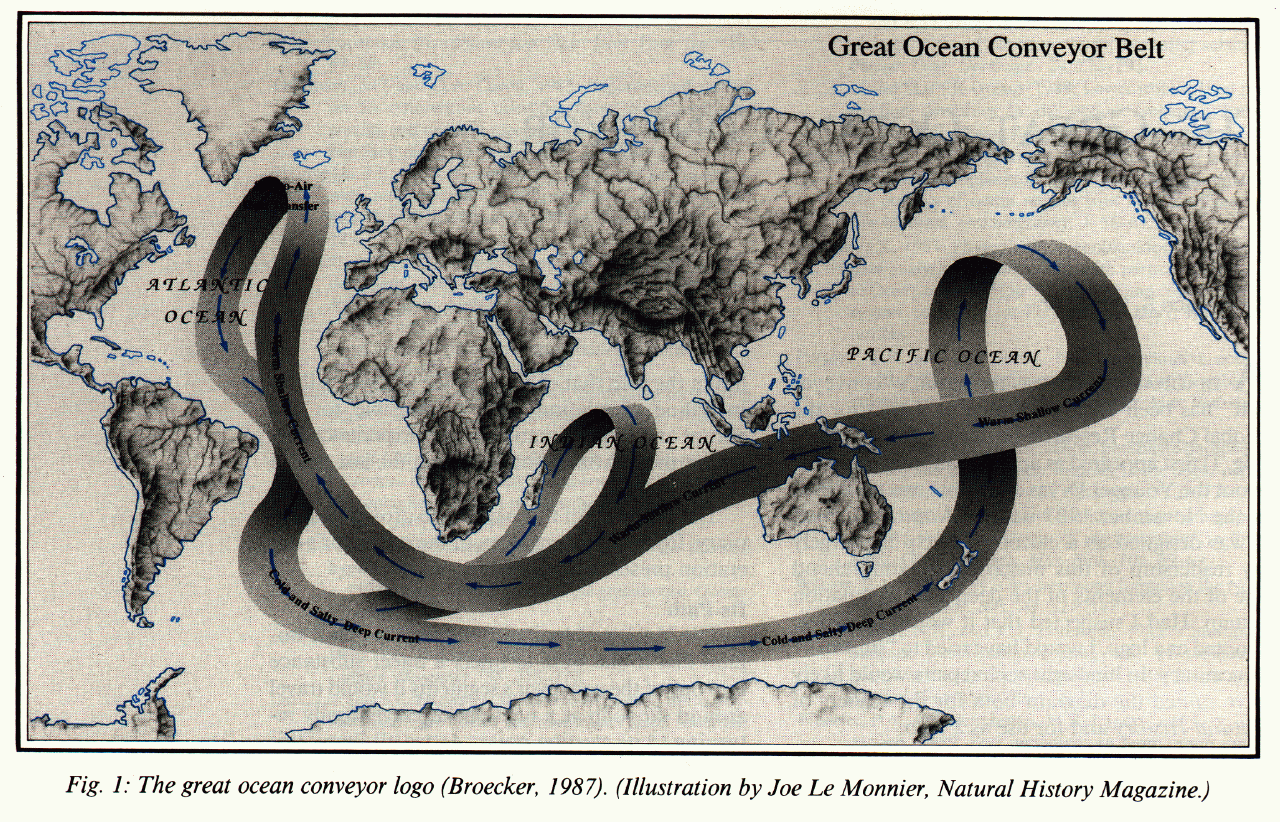
Ocean: History
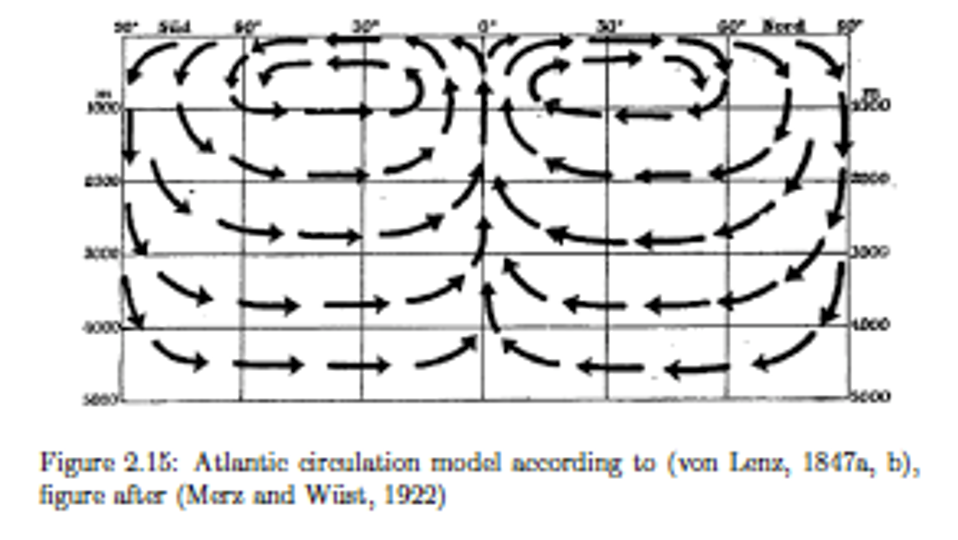
Conveyor Belt

Conveyor belt: climate change
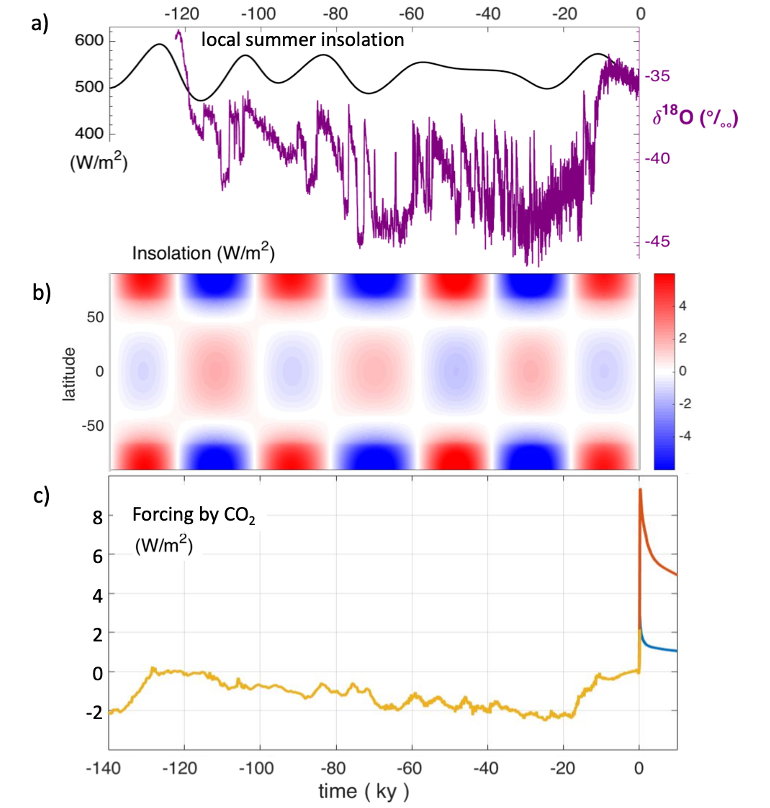
halting or reversing the ocean circulation
interpretation of Greenland ice core records
climate states with different ocean modes
Overturning Circulation (model)
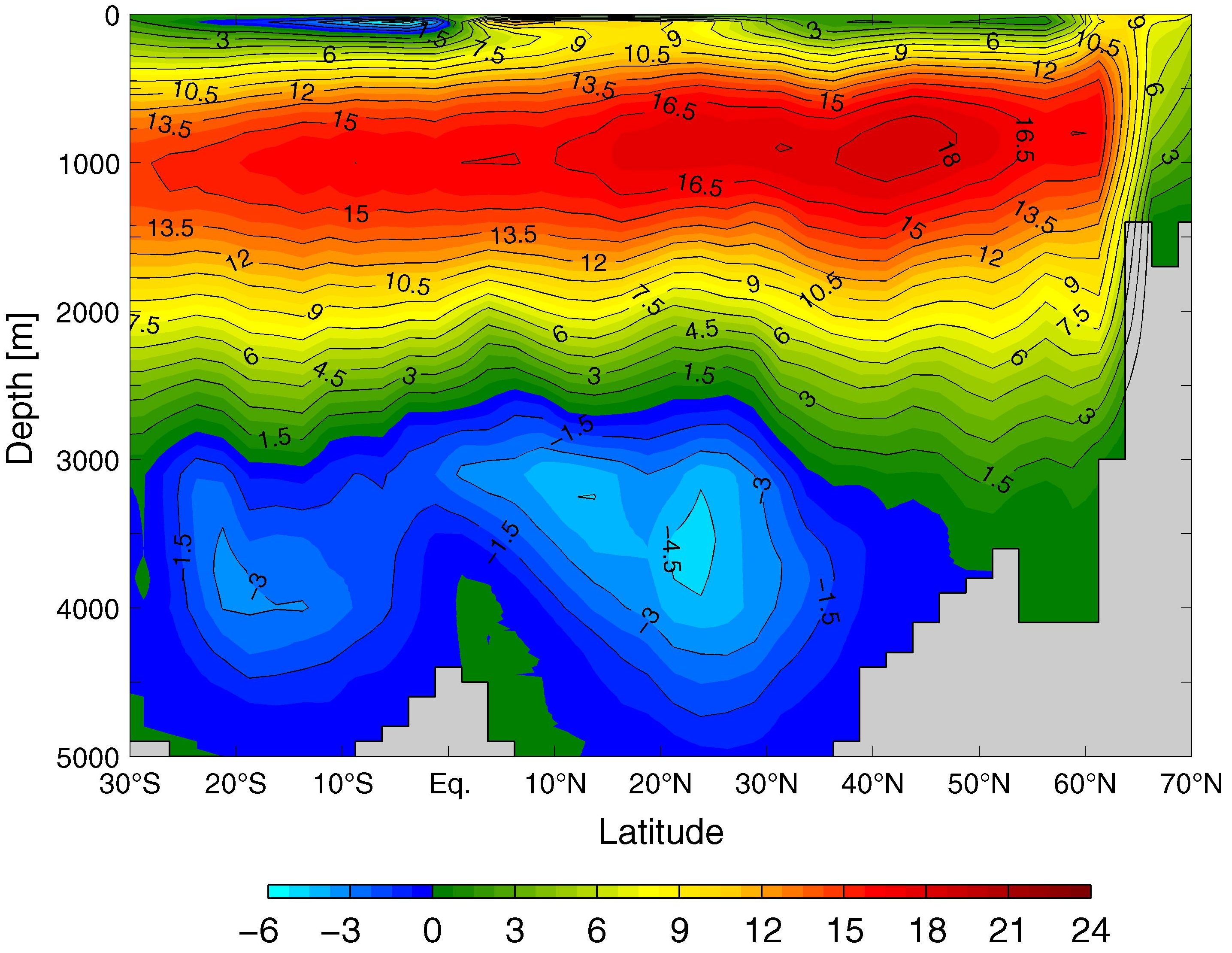 Modelled meridional overturning streamfunction in Sv 106 = m3 /s in the Atlantic Ocean. Grey areas represent zonally integrated smoothed bathymetry
Modelled meridional overturning streamfunction in Sv 106 = m3 /s in the Atlantic Ocean. Grey areas represent zonally integrated smoothed bathymetry
Atlantic water masses
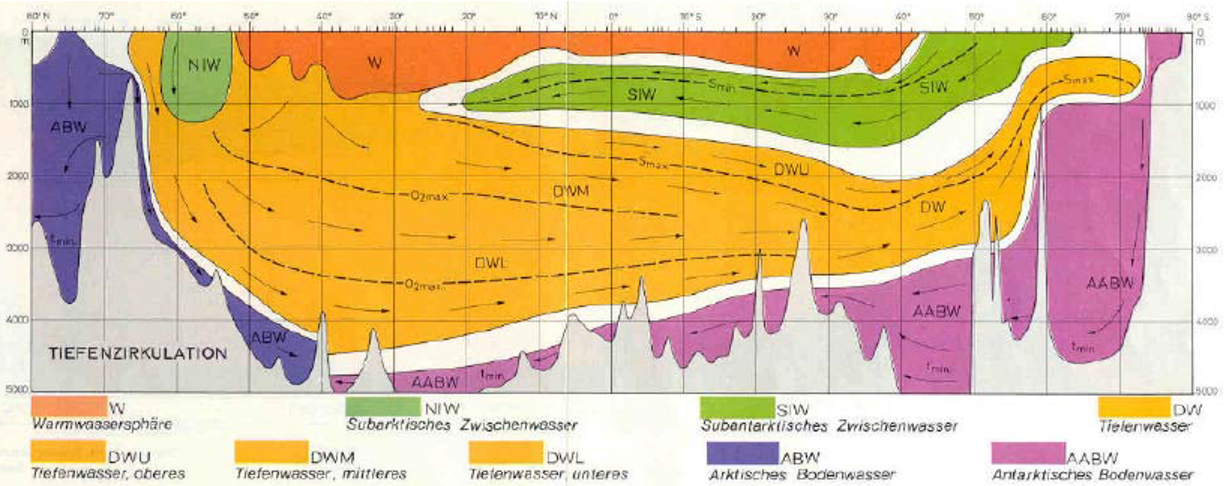
North
Estimates of overturning
Timescale T to 'fill up' the Atlantic basin:
\[ T = \frac{ 80 \cdot 10^{12} \, m^2 \cdot 4000 \, m}{15 \cdot 10^6 \, m^3 s^{-1}} = 2.13 \cdot 10^{10} s = 676 \;years \]
Overturning is balanced by large-scale upwelling:
\[ area \cdot w = 15 \cdot 10^6 \, m^3 s^{-1} \]
\[ w = 0.1875 \cdot 10^{-6} m\;s^{-1} = 5.9 \cdot 10^{-15} m \; y^{-1}. \]
compare to Ekman pumping \[ w_E \simeq 32 \, \, m \; y^{-1}. \]
Vorticity dynamics of meridional overturning (y,z)
\[ \frac{\partial}{\partial t} v \quad = \quad - \frac{1}{\rho_0} \frac{\partial p}{\partial y} \quad - \quad f u \quad - \quad \kappa v \]
\[ \frac{\partial}{\partial t} w \quad = \quad - \frac{1}{\rho_0} \frac{\partial p}{\partial z} \quad - \quad \frac{g}{\rho_0} (\rho -\rho_0) \quad - \quad \kappa w \] \( \kappa \) as parameter for Rayleigh friction.
Amplitude of overturning
\[ \frac{d}{dt} \Phi_{max} \, = \, \frac{a}{\rho_0} (\rho_{north} - \rho_{south}) \, \, - \, \, \kappa \Phi_{max} \] with \[ a = g L H^2/4(L^2 + H^2) \, \]
This shows that the overturning circulation depends on the density differences on the right and left boxes.
It is simplified to a diagnostic relation
\[ \Phi_{max} = \frac{a}{\rho_0 \, \kappa} \, \, (\rho_{north} - \rho_{south}) \quad \]
because the adjustment of \( \Phi_{max} \) is quasi-instantaneous due to adjustment processes, e.g. Kelvin waves.
North-south density gradient in an ocean basin
Primary north-south gradient in balance with an eastward geostrophic current: generates a secondary high & low pressure system, northward current
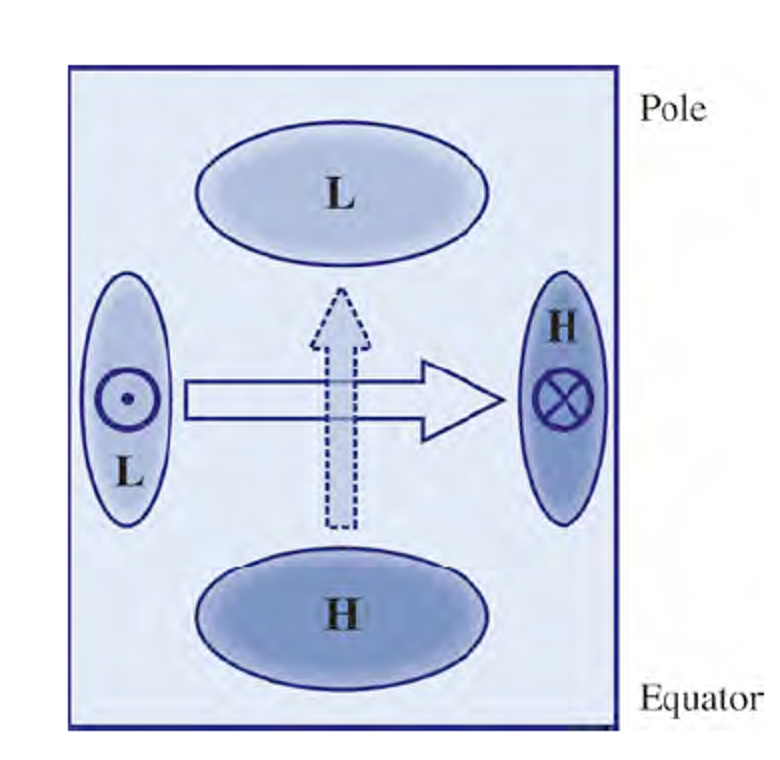
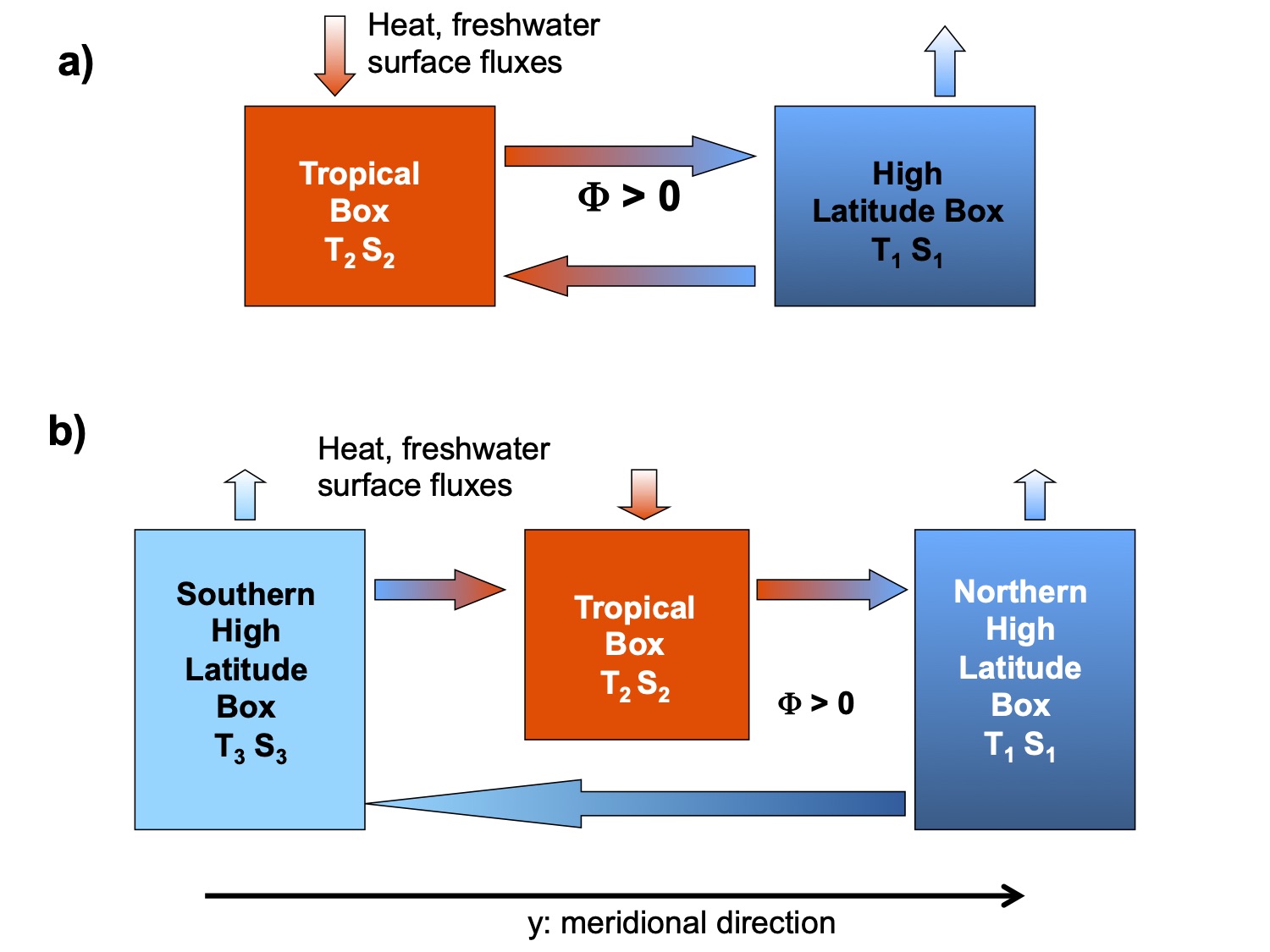
Schematic picture of the hemispheric two box model (a) and of the interhemispheric box model
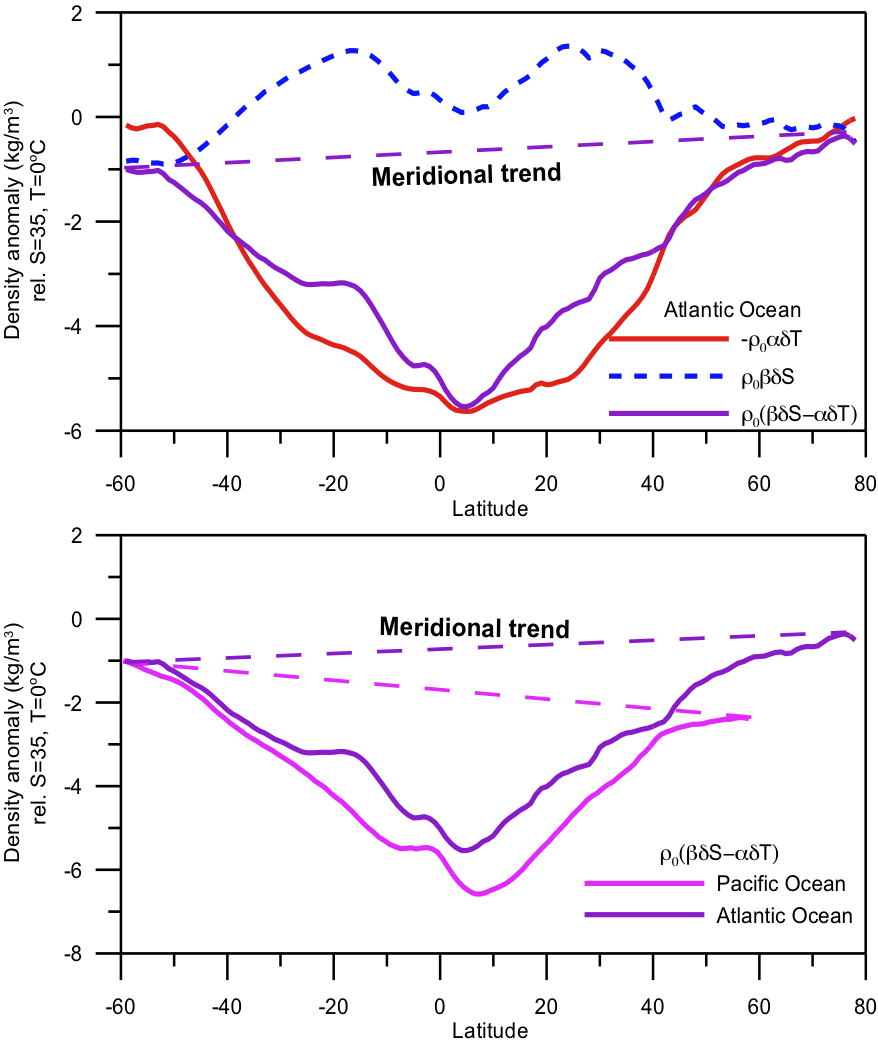
a) The Atlantic surface density is mainly related to temperature differences. b) But the pole-to-pole differences are caused by salinity differences. }
Box model of the thermohaline circulation
hemispheric (Stommel-type) or interhemispheric (Rooth-type)
\[ \Phi \, = \, - c \, ( \alpha \Delta T - \beta \Delta S ) \qquad , \] where \( \alpha \) and \( \beta \) are the thermal and haline expansion coefficients,
\( \Delta \) denotes the meridional difference operator applied to temperature T and salinity S, respectively.
single hemispheric view:
The meridional density differences are clearly dominated by temperature
Salinity difference breakes the temperature difference
both hemispheres:
densities at high northern and southern latitudes are close,
the pole-to-pole differences are caused by salinity differences.
Ocean: multiple equilibria in GCM
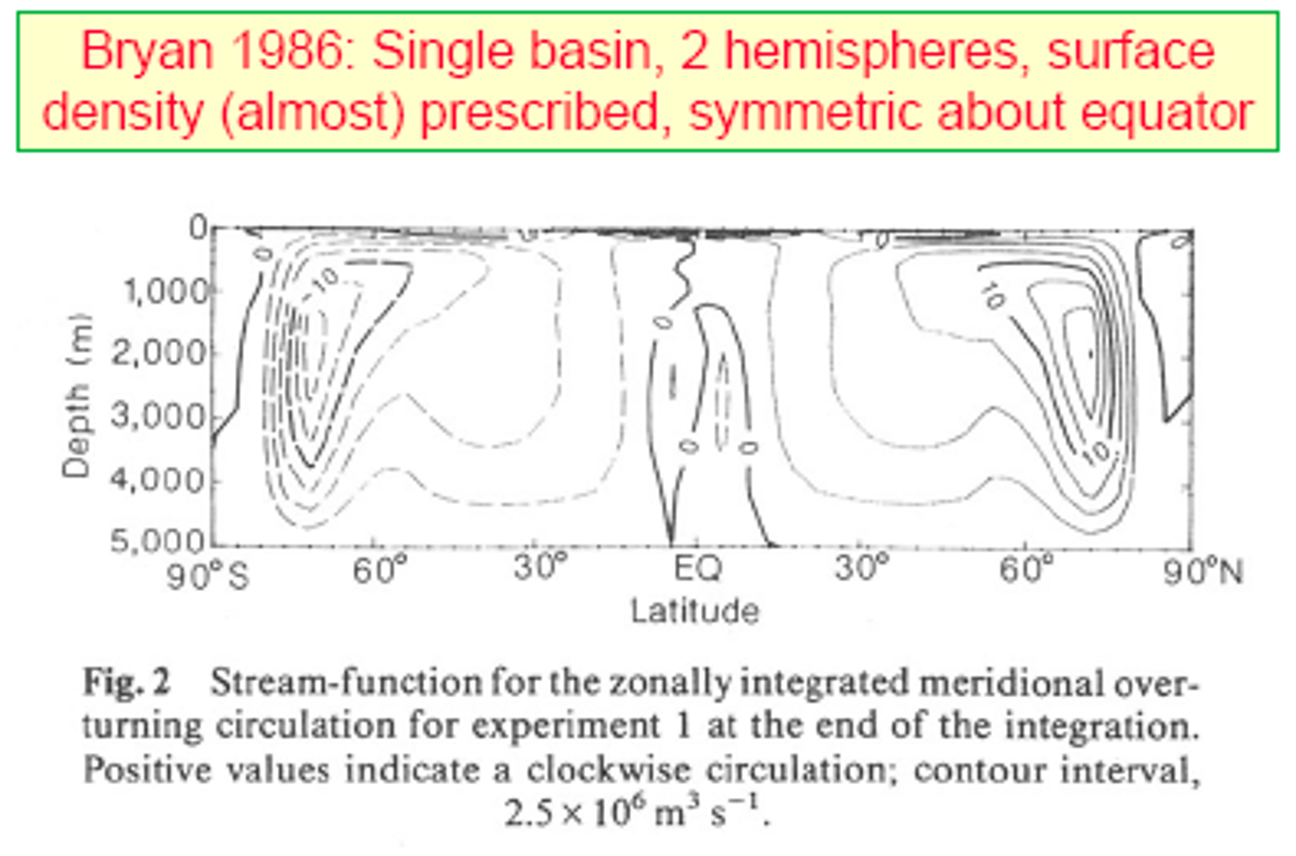
Ocean: multiple equilibria in GCM
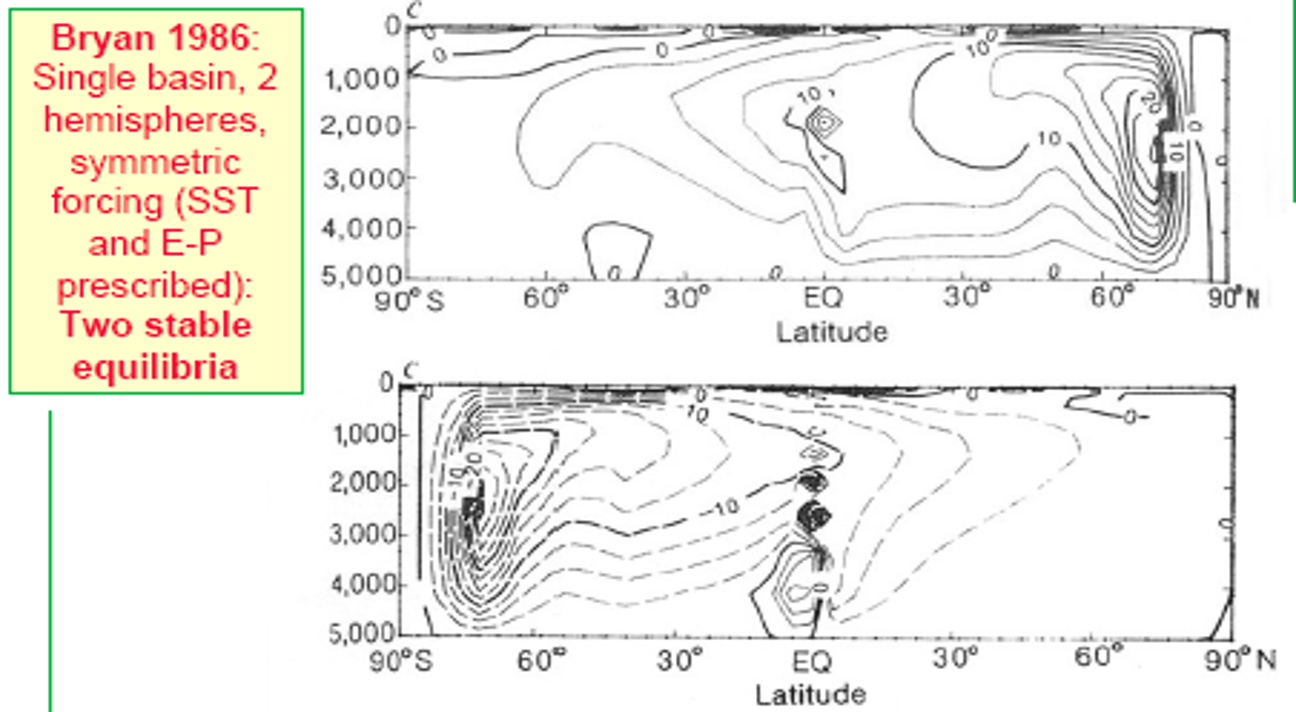
Ocean response: Hosing the North Atlantic
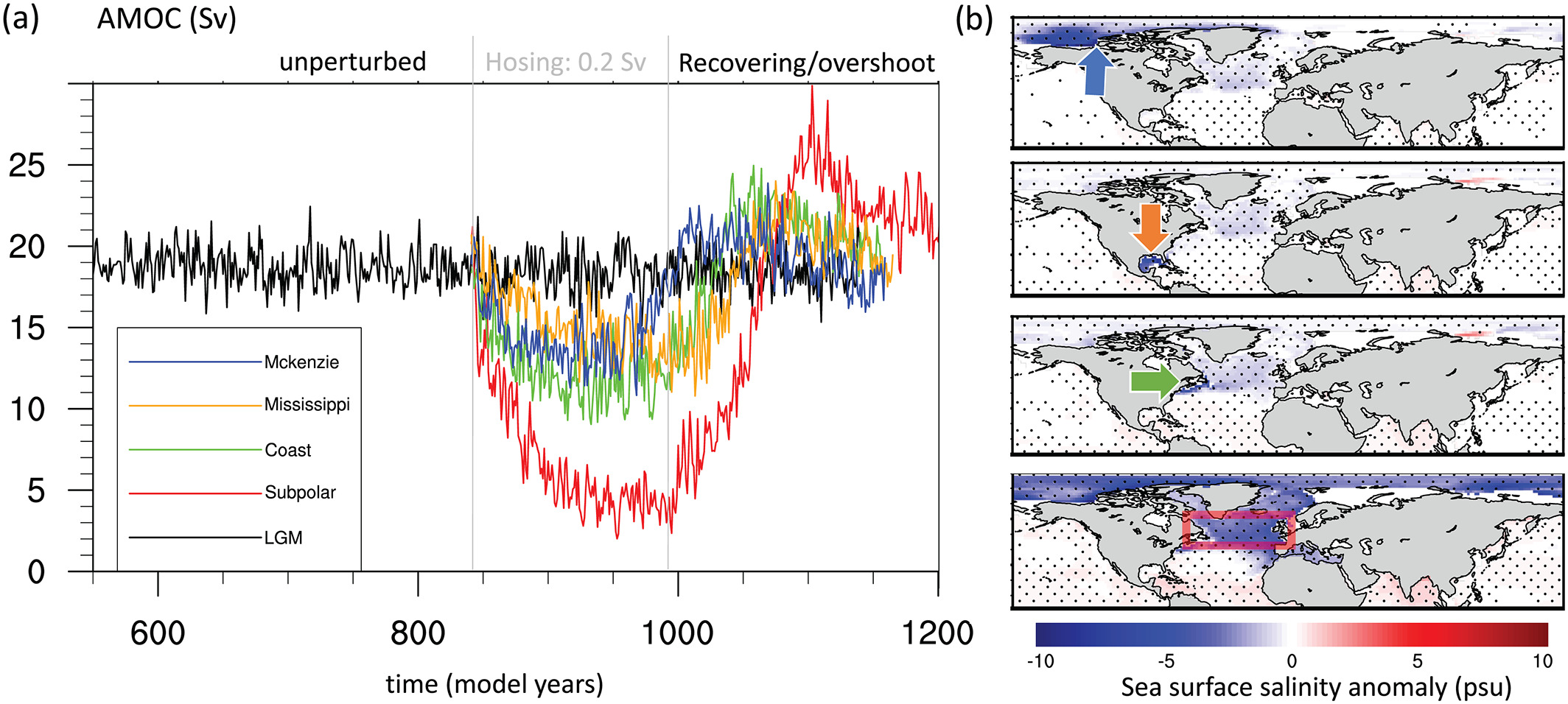
(a) AMOC indices of North Atlantic hosing for different hosing areas. Units are Sv. Black line represents the unperturbed LGM experiment. Hosing is for the period 840–990. (b) Annual mean sea surface salinity anomaly between LGM and the perturbation experiment LGM with 0.2 Sv for the model years 900–950.
-> Multi-scale Ocean GCM
Conveyor belt: climate change

halting or reversing the ocean circulation
interpretation of Greenland ice core records
climate states with different ocean modes
Abrupt climate change, termination of ice sheets, Climate System II
Ocean box model
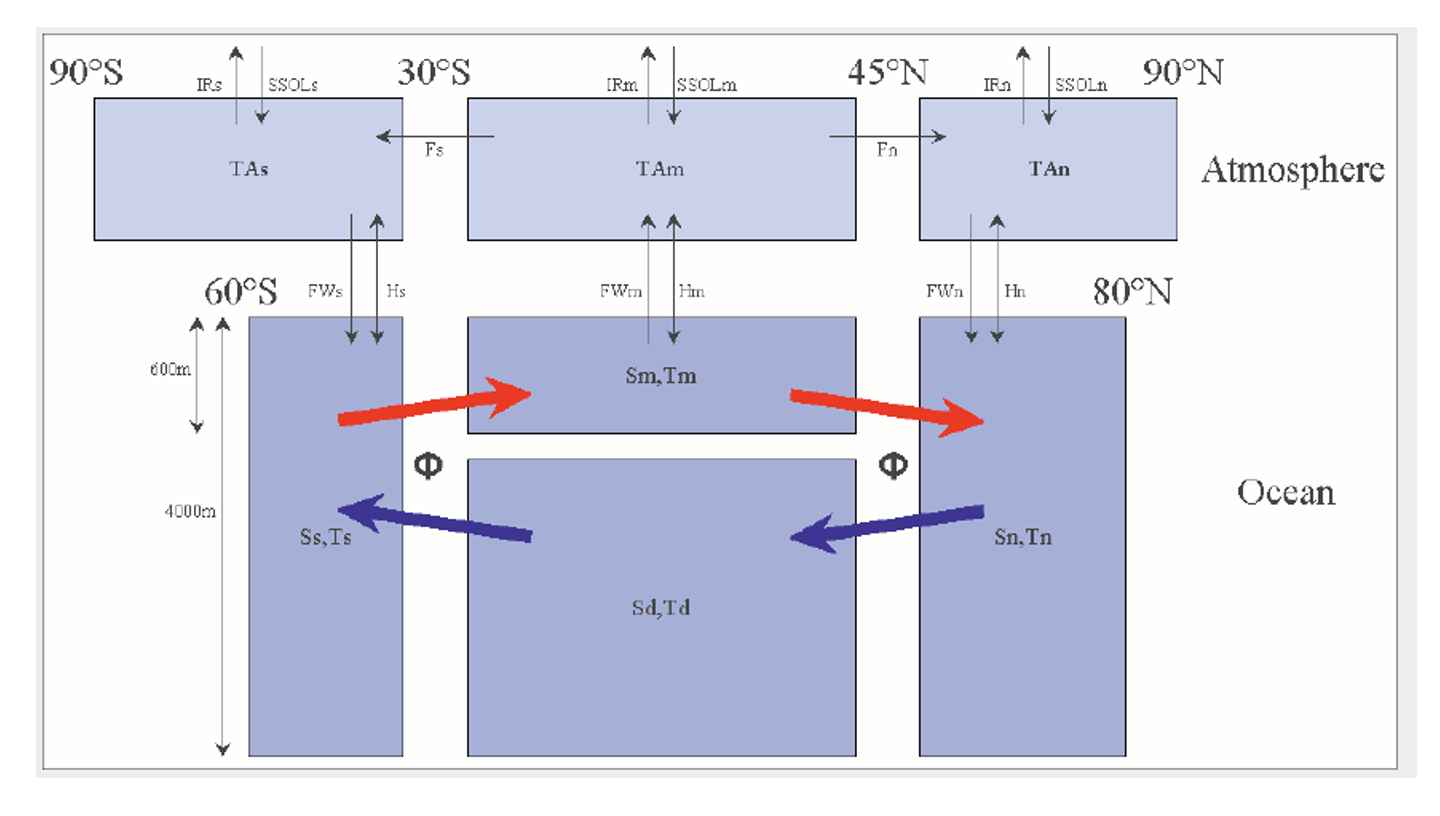
Ocean: Temperature

Euler forward for ocean temperature
Tnln = Tnl + dts * ((Hfnl)/(rcz2)-(Tnl-Tml)*phi/Vnl);
Tmln = Tml + dts * ((Hfml)/(rcz1)-(Tml-Tsl)*phi/Vml);
Tsln = Tsl + dts * ((Hfsl)/(rcz2)-(Tsl-Td)*phi/Vsl);
Tdn = Td + dts * (-(Td-Tnl)*(phi/Vd));
Atmosphere

Boxmodel
Download link password: DynamicsII2020
1) go to the folder where the boxmodel is located (ui.R): setwd(' … ')
2) install.packages(“shiny”)
3) library(shiny)
4) runApp()
5) a browser window should open that displays the boxmodel controls
6) first click on the button Spin-Up to create a new spin up
7) a new window opens, click on Run SpinUp
8) afterwards click on Apply, then Cancel
9) define parameters for the model simulation
10) run the simulation by clicking on Start Simulation